In mathematics, an even function is a real function such that for every in its domain. Similarly, an odd function is a function such that for every in its domain.


They are named for the parity of the powers of the power functions which satisfy each condition: the function is even if n is an even integer, and it is odd if n is an odd integer.
Even functions are those real functions whose graph is self-symmetric with respect to the y-axis, and odd functions are those whose graph is self-symmetric with respect to the origin.
If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely decomposed as the sum of an even function and an odd function.
Definition and examples
Evenness and oddness are generally considered for real functions, that is real-valued functions of a real variable. However, the concepts may be more generally defined for functions whose domain and codomain both have a notion of additive inverse. This includes abelian groups, all rings, all fields, and all vector spaces. Thus, for example, a real function could be odd or even (or neither), as could a complex-valued function of a vector variable, and so on.
The given examples are real functions, to illustrate the symmetry of their graphs.
Even functions
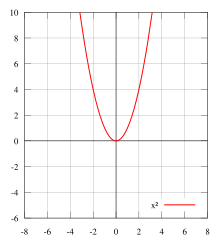
 is an example of an even function.
is an example of an even function.Let f be a real-valued function of a real variable. Then f is even if the following equation holds for all x such that x and −x are in the domain of f:[1]: p. 11
or equivalently if the following equation holds for all such x:
Geometrically, the graph of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis.
Examples of even functions are:
Odd functions

 is an example of an odd function.
is an example of an odd function.Again, let f be a real-valued function of a real variable. Then f is odd if the following equation holds for all x such that x and −x are in the domain of f:[1]: p. 72
or equivalently if the following equation holds for all such x:
Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin.
Examples of odd functions are:
- The sign function
- The identity function
- sine
- hyperbolic sine
- The error function
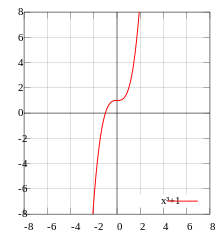
 is neither even nor odd.
is neither even nor odd.Basic properties
Uniqueness
- If a function is both even and odd, it is equal to 0 everywhere it is defined.
- If a function is odd, the absolute value of that function is an even function.
Addition and subtraction
- The sum of two even functions is even.
- The sum of two odd functions is odd.
- The difference between two odd functions is odd.
- The difference between two even functions is even.
- The sum of an even and odd function is not even or odd, unless one of the functions is equal to zero over the given domain.
Multiplication and division
- The product of two even functions is an even function.
- That implies that product of any number of even functions is an even function as well.
- The product of two odd functions is an even function.
- The product of an even function and an odd function is an odd function.
- The quotient of two even functions is an even function.
- The quotient of two odd functions is an even function.
- The quotient of an even function and an odd function is an odd function.
Composition
- The composition of two even functions is even.
- The composition of two odd functions is odd.
- The composition of an even function and an odd function is even.
- The composition of any function with an even function is even (but not vice versa).
Even–odd decomposition
Every function may be uniquely decomposed as the sum of an even and an odd function, which are called respectively the even part and the odd part of the function; if one defines
and










































