 An alternated square tiling or checkerboard pattern. |  An expanded square tiling. |
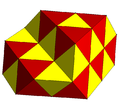 A partially filled alternated cubic honeycomb with tetrahedral and octahedral cells. | 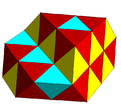 A subsymmetry colored alternated cubic honeycomb. |
In geometry, the alternated hypercube honeycomb (or demicubic honeycomb) is a dimensional infinite series of honeycombs, based on the hypercube honeycomb with an alternation operation. It is given a Schläfli symbol h{4,3...3,4} representing the regular form with half the vertices removed and containing the symmetry of Coxeter group for n ≥ 4. A lower symmetry form can be created by removing another mirror on an order-4 peak.[1]
The alternated hypercube facets become demihypercubes, and the deleted vertices create new orthoplex facets. The vertex figure for honeycombs of this family are rectified orthoplexes.
These are also named as hδn for an (n-1)-dimensional honeycomb.
| hδn | Name | Schläfli symbol | Symmetry family | ||
|---|---|---|---|---|---|
[4,3n-4,31,1] | [31,1,3n-5,31,1] | ||||
| Coxeter-Dynkin diagrams by family | |||||
| hδ2 | Apeirogon | {∞} | |||
| hδ3 | Alternated square tiling (Same as {4,4}) | h{4,4}=t1{4,4} t0,2{4,4} | |||
| hδ4 | Alternated cubic honeycomb | h{4,3,4} {31,1,4} | |||
| hδ5 | 16-cell tetracomb (Same as {3,3,4,3}) | h{4,32,4} {31,1,3,4} {31,1,1,1} | |||
| hδ6 | 5-demicube honeycomb | h{4,33,4} {31,1,32,4} {31,1,3,31,1} | |||
| hδ7 | 6-demicube honeycomb | h{4,34,4} {31,1,33,4} {31,1,32,31,1} | |||
| hδ8 | 7-demicube honeycomb | h{4,35,4} {31,1,34,4} {31,1,33,31,1} | |||
| hδ9 | 8-demicube honeycomb | h{4,36,4} {31,1,35,4} {31,1,34,31,1} | |||
| hδn | n-demicubic honeycomb | h{4,3n-3,4} {31,1,3n-4,4} {31,1,3n-5,31,1} | ... | ||
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- pp. 122–123, 1973. (The lattice of hypercubes γn form the cubic honeycombs, δn+1)
- pp. 154–156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}
- p. 296, Table II: Regular honeycombs, δn+1
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
| Space | Family |  |  |  |  |  / /  / /  |
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | {3[11]} | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
🔥 Top keywords: Main PageSpecial:SearchWikipedia:Featured picturesYasukeHarrison ButkerRobert FicoBridgertonCleopatraDeaths in 2024Joyce VincentXXXTentacionHank AdamsIt Ends with UsYouTubeNew Caledonia2024 Indian general electionHeeramandiDarren DutchyshenSlovakiaKingdom of the Planet of the ApesAttempted assassination of Robert FicoLawrence WongBaby ReindeerXXX: Return of Xander CageThelma HoustonFuriosa: A Mad Max SagaMegalopolis (film)Richard GaddKepler's SupernovaWicked (musical)Sunil ChhetriXXX (2002 film)Ashley MadisonAnya Taylor-JoyPlanet of the ApesNava MauYoung SheldonPortal:Current eventsX-Men '97