| Part of a series on Statistics |
| Random variables |
|---|
Correlation and covariance of random vectors |
Correlation and covariance of stochastic processes |
Distribution functions |
Documentation
Category:Sidebar templatesCategory:Statistics templatesCategory:Sidebar templates by topic
| Part of a series on Statistics |
| Stochastic processes |
|---|
Correlation and covariance of random vectors
|
Correlation and covariance of stochastic processes |
Distribution functions |
Documentation
Category:Sidebar templatesCategory:Statistics templatesCategory:Sidebar templates by topic
Symmetry properties

- If is a real function, then (Hermitian symmetric) which implies:
- (real part is even symmetric)
- (imaginary part is odd symmetric)
- (absolut value is even symmetric)
- (argument is odd symmetric)
- If is a real and even function (), then all coefficients are real and (even symmetric) which implies:
- for all
- If is a real and odd function (), then all coefficients are purely imaginary and (odd symmetric) which implies:
- for all
- If is a purely imaginary function, then which implies:
- (real part is odd symmetric)
- (imaginary part is even symmetric)
- (absolut value is even symmetric)
- (argument is odd symmetric)
- If is a purely imaginary and even function (), then all coefficients are purely imaginary and (even symmetric).
- If is a purely imaginary and odd function (), then all coefficients are real and (odd symmetric).
Table of Fourier Series coefficients
Some common pairsof periodic functions and their Fourier Series coefficients are shown in the table below. The following notation applies:
designates a periodic function defined on
.
designates a ...
designates a ...
Time domain  | Plot | Frequency domain (sine-cosine form)  | Remarks | Reference |
|---|---|---|---|---|
 |  |  | Full-wave rectified sine | [1]: p. 193 |
 |  |  | Full-wave rectified sine cut by a phase-fired controller | |
 | 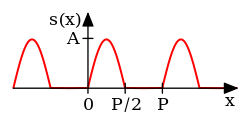 |  | Half-wave rectified sine | [1]: p. 193 |
 |  |  |  | |
 | 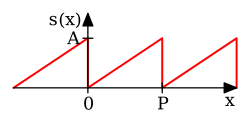 |  | [1]: p. 192 | |
 |  |  | [1]: p. 192 | |
 |  |  | [1]: p. 193 | |
 |  |  |  | |
 |  |  |  | |
 |  denotes the Dirac delta function. denotes the Dirac delta function. |
Properties
This table shows some mathematical operations in the time domain and the corresponding effects in the frequency domain.
is the complex conjugate of
.
designate a
-periodic functions defined on
.
designates the Fourier series coefficients (exponential form) of
and
as defined in equation TODO!!!
| Property | Time domain | Frequency domain (exponential form) | Remarks | Reference |
|---|---|---|---|---|
| Linearity |  |  | complex numbers  | |
| Time reversal / Frequency reversal |  |  | [2]: p. 610 | |
| Time conjugation |  |  | [2]: p. 610 | |
| Time reversal & conjugation |  |  | ||
| Real part in time |  |  | ||
| Imaginary part in time |  |  | ||
| Real part in frequency |  |  | ||
| Imaginary part in frequency |  |  | ||
| Shift in time / Modulation in frequency |  |  | real number  | [2]: p. 610 |
| Shift in frequency / Modulation in time |  |  | integer  | [2]: p. 610 |
| Differencing in frequency | ||||
| Summation in frequency | ||||
| Derivative in time |  |  | ||
Derivative in time ( times) times) | ||||
| Integration in time | ||||
| Convolution in time / Multiplication in frequency |  |  |  denotes continuous circular convolution. denotes continuous circular convolution. | |
| Multiplication in time / Convolution in frequency |  |  |  denotes Discrete convolution. denotes Discrete convolution. | |
| Cross correlation |  |  | ||
| Parseval's theorem |  |  | [3]: p. 236 |
🔥 Top keywords: Main PageSpecial:SearchWikipedia:Featured picturesYasukeHarrison ButkerRobert FicoBridgertonCleopatraDeaths in 2024Joyce VincentXXXTentacionHank AdamsIt Ends with UsYouTubeNew Caledonia2024 Indian general electionHeeramandiDarren DutchyshenSlovakiaKingdom of the Planet of the ApesAttempted assassination of Robert FicoLawrence WongBaby ReindeerXXX: Return of Xander CageThelma HoustonFuriosa: A Mad Max SagaMegalopolis (film)Richard GaddKepler's SupernovaWicked (musical)Sunil ChhetriXXX (2002 film)Ashley MadisonAnya Taylor-JoyPlanet of the ApesNava MauYoung SheldonPortal:Current eventsX-Men '97


















