Pengguna:Kekavigi/bak pasir baru

Pada tahun 1563, Arbermouth Holst memperkenalkan bilangan bulat ketika sedang menghitung jumlah kelinci di dalam kandangnya dan setelah 6 bulan telah menemukan bahwa jumlah kelincinya meningkat.^[6]

Beliau menemukan sistem bilangan terhadap penambahan dan perkalian dan menghabiskan waktu selama 15 tahun untuk mengembangkan sistem bilangan tersebut.^[6]

Pada tahun 1890, matematikawan Jepang bekerja pada bilangan tersebut dan menciptakan bilangan bulat, dari bahasa Latin, integer, yang berarti "tidak tersentuh".^[6]

To give but a few examples of the problems: In the subject "First use of numbers" the Mesopotamian sexagesimal place value system is dated to 3400 BC, whereas the linked article dates it to 2100 BC, which seems much closer to dates I have seen in the scholarly literature. The second half of the passage could be read as saying that the Egyptian system was also a place-value system, which it was not.

In the first paragraph on the history of irrational numbers just about every statement is either false or misleading. The opening sentence says the oldest known use of irrational numbers was in the Sulba Sutras (800 BC – 500 BC). The Shulba Sutras do contain approximations of the square root of 2, but do not mention the concept of irrationality. Furthermore, the square root of 2 had been approximated just about as accurately 1000 years earlier in Mesopotamia. The rest of the paragraph consists of an uncritical presentation of the most sensationalistic version of the Hipassus myth. The ancient sources for the myth were written more than half a millennium after the time of Pythagoras and are considered unreliable. Not all mention Hippasus; not all mention death by drowning; they don't agree that the infraction was related to the discovery of irrationality; the story of Pythagoras issuing a death sentence is, as far as I can tell, a modern invention. Furthermore, numbers for the ancient Greeks were 2, 3, 4, ... They had theories of ratios, both of numbers and of magnitudes, and had proved that some magnitudes were incommensurable, but they did not manipulate ratios arithmetically as numbers.

Numeral systems have progressed from the use of tally marks, more than 40,000 years ago, through to the use of sets of glyphs to efficiently represent any conceivable number.

Tulang Lebombo, Tulang Ishango, Tongkat hitungan

The first method of counting has been argued to be counting on fingers.^{[7][butuh sumber yang lebih baik]} This evolved into sign language for the hand-to-eye-to-elbow communication of numbers which, while not writing, gave way to written numbers.

Tallies made by carving notches in wood, bone, and stone were used for at least forty thousand years.^[8][9] These tally marks may have been used for counting elapsed time, such as numbers of days, lunar cycles or keeping records of quantities, such as of animals.

Lebombo bone is a baboon fibula with incised markings discovered in the Lebombo Mountains located between South Africa and Eswatini. The bone is between 44,230 and 43,000 years old, according to two dozen radiocarbon datings. According to The Universal Book of Mathematics the Lebombo bone's 29 notches suggest "it may have been used as a lunar phase counter, in which case African women may have been the first mathematicians, because keeping track of menstrual cycles requires a lunar calendar." But the bone is clearly broken at one end, so the 29 notches can only be a minimum number. Furthermore, in the many more notched bones since found there is no consistent notch tally, many being in the 1–10 range.

Ishango bone is an artifact with a sharp piece of quartz affixed to one end, perhaps for engraving. It was first thought to be a tally stick, as it has a series of what has been interpreted as tally marks carved in three columns running the length of the tool. But some scientists have suggested that the groupings of notches indicate a mathematical understanding that goes beyond counting. It has also been suggested that the scratches might have been to create a better grip on the handle or for some other non-mathematical reason. It is believed that the bone is more than 20,000 years old.^[10][11]

The earliest known writing for record keeping evolved from a system of counting using small clay tokens. The earliest tokens now known are those from two sites in the Zagros region of Iran: Tepe Asiab and Ganj-i-Dareh Tepe.^[12]

To create a record that represented "two sheep", they selected two round clay tokens each having a + sign baked into it. Each token represented one sheep. Representing a hundred sheep with a hundred tokens would be impractical, so they invented different clay tokens to represent different numbers of each specific commodity, and by 4000 BC strung the tokens like beads on a string.^[13] There was a token for one sheep, a different token for ten sheep, a different token for ten goats, etc. Thirty-two sheep would be represented by three ten-sheep tokens followed on the string by two one-sheep tokens.

To ensure that nobody could alter the number and type of tokens, they invented a clay envelope shaped like a hollow ball (a bulla) into which the tokens on a string were placed, sealed, and baked. If anybody disputed the number, they could break open the clay envelope and do a recount. To avoid unnecessary damage to the record, they pressed archaic number signs and witness seals on the outside of the envelope before it was baked, each sign similar in shape to the tokens they represented. Since there was seldom any need to break open the envelope, the signs on the outside became the first written language for writing numbers in clay. An alternative method was to seal the knot in each string of tokens with a solid oblong bulla of clay having impressed symbols, while the string of tokens dangled outside of the bulla.^[14]

Beginning about 3500 BC the tokens and envelopes were replaced by numerals impressed with a round stylus at different angles in flat clay tablets which were then baked.^[15] A sharp stylus was used to carve pictographs representing various tokens. Each sign represented both the commodity being counted and the quantity or volume of that commodity.

Abstract numerals, dissociated from the thing being counted, were invented about 3100 BC.^[16] The things being counted were indicated by pictographs carved with a sharp stylus next to round-stylus numerals.

The Sumerians had a complex assortment of incompatible number systems, and each city had its own local way of writing numerals. For instance, at about 3100 BC in the city of Uruk, there were more than a dozen different numeric systems.^[17] In this city, there were separate number systems for counting discrete objects (such as animals, tools, and containers), cheese and grain products, volumes of grain (including fractions), beer ingredients, weights, land areas, and time and calendar units. Furthermore, these systems changed over time; for instance, numbers for counting volumes of grain changed when the size of the baskets changed.

The Sumerians invented arithmetic.^[18] People who added and subtracted volumes of grain every day used their arithmetic skills to count other things that were unrelated to volume measurements. Multiplication and division were done with multiplication tables baked in clay tablets.^[19]

Between 2700 BC and 2000 BC, the round stylus was gradually replaced by a reed stylus that had been used to press wedge shaped cuneiform signs in clay. To represent numbers that previously had been pressed with a round stylus, these cuneiform number signs were pressed in a circular pattern and they retained the additive sign-value notation that originated with tokens on a string. Cuneiform numerals and archaic numerals were ambiguous because they represented various numeric systems that differed depending on what was being counted. About 2100 BC in Sumer, these proto-sexagesimal sign-value systems gradually converged on a common sexagesimal number system that was a place-value system consisting of only two impressed marks, the vertical wedge and the chevron, which could also represent fractions.^[20] This sexagesimal number system was fully developed at the beginning of the Old Babylonian period (about 1950 BC) and became standard in Babylonia.

Sexagesimal numerals were a mixed radix system that retained the alternating base 10 and base 6 in a sequence of cuneiform vertical wedges and chevrons. Sexagesimal numerals became widely used in commerce, but were also used in astronomical and other calculations. This system was exported from Babylonia and used throughout Mesopotamia, and by every Mediterranean nation that used standard Babylonian units of measure and counting, including the Greeks, Romans and Syrians. In Arabic numerals, we still use sexagesimal to count time (minutes per hour), and angles (degrees).

Roman numerals evolved from this primitive system of cutting notches.^[21] It was once believed that they came from alphabetic symbols or from pictographs, but these theories have been disproved.^[22][23]

The most commonly used system of numerals is decimal. Indian mathematicians are credited with developing the integer version, the Hindu–Arabic numeral system.^[24] Aryabhata of Kusumapura developed the place-value notation in the 5th century and a century later Brahmagupta introduced the symbol for zero. The system slowly spread to other surrounding regions like Arabia due to their commercial and military activities with India. Middle-Eastern mathematicians extended the system to include negative powers of 10 (fractions), as recorded in a treatise by Syrian mathematician Abu'l-Hasan al-Uqlidisi in 952–953, and the decimal point notation was introduced^{[per kapan?]} by Sind ibn Ali, who also wrote the earliest treatise on Arabic numerals. The Hindu-Arabic numeral system then spread to Europe due to merchants trading, and the digits used in Europe are called Arabic numerals, as they learned them from the Arabs.

The simplest numeral system is the unary numeral system, in which every natural number is represented by a corresponding number of symbols. If the symbol / is chosen, for example, then the number seven would be represented by ///////. Tally marks represent one such system still in common use. The unary system is only useful for small numbers, although it plays an important role in theoretical computer science. Elias gamma coding, which is commonly used in data compression, expresses arbitrary-sized numbers by using unary to indicate the length of a binary numeral.

The unary notation can be abbreviated by introducing different symbols for certain new values. Very commonly, these values are powers of 10; so for instance, if / stands for one, − for ten and + for 100, then the number 304 can be compactly represented as +++ //// and the number 123 as + − − /// without any need for zero. This is called sign-value notation. The ancient Egyptian numeral system was of this type, and the Roman numeral system was a modification of this idea.

More useful still are systems which employ special abbreviations for repetitions of symbols; for example, using the first nine letters of the alphabet for these abbreviations, with A standing for "one occurrence", B "two occurrences", and so on, one could then write C+ D/ for the number 304. This system is used when writing Chinese numerals and other East Asian numerals based on Chinese. The number system of the English language is of this type ("three hundred [and] four"), as are those of other spoken languages, regardless of what written systems they have adopted. However, many languages use mixtures of bases, and other features, for instance 79 in French is soixante dix-neuf (60 + 10 + 9) and in Welsh is pedwar ar bymtheg a thrigain (4 + (5 + 10) + (3 × 20)) or (somewhat archaic) pedwar ugain namyn un (4 × 20 − 1). In English, one could say "four score less one", as in the famous Gettysburg Address representing "87 years ago" as "four score and seven years ago".

More elegant is a positional system, also known as place-value notation. Again working in base 10, ten different digits 0, ..., 9 are used and the position of a digit is used to signify the power of ten that the digit is to be multiplied with, as in 304 = 3×100 + 0×10 + 4×1 or more precisely 3×10² + 0×10¹ + 4×10⁰. Zero, which is not needed in the other systems, is of crucial importance here, in order to be able to "skip" a power. The Hindu–Arabic numeral system, which originated in India and is now used throughout the world, is a positional base 10 system.

Arithmetic is much easier in positional systems than in the earlier additive ones; furthermore, additive systems need a large number of different symbols for the different powers of 10; a positional system needs only ten different symbols (assuming that it uses base 10).^[25]

The positional decimal system is presently universally used in human writing. The base 1000 is also used (albeit not universally), by grouping the digits and considering a sequence of three decimal digits as a single digit. This is the meaning of the common notation 1,000,234,567 used for very large numbers.

In computers, the main numeral systems are based on the positional system in base 2 (binary numeral system), with two binary digits, 0 and 1. Positional systems obtained by grouping binary digits by three (octal numeral system) or four (hexadecimal numeral system) are commonly used. For very large integers, bases 2³² or 2⁶⁴ (grouping binary digits by 32 or 64, the length of the machine word) are used, as, for example, in GMP.

In certain biological systems, the unary coding system is employed. Unary numerals used in the neural circuits responsible for birdsong production.^[26] The nucleus in the brain of the songbirds that plays a part in both the learning and the production of bird song is the HVC (high vocal center). The command signals for different notes in the birdsong emanate from different points in the HVC. This coding works as space coding which is an efficient strategy for biological circuits due to its inherent simplicity and robustness.

The numerals used when writing numbers with digits or symbols can be divided into two types that might be called the arithmetic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and the geometric numerals (1, 10, 100, 1000, 10000 ...), respectively. The sign-value systems use only the geometric numerals and the positional systems use only the arithmetic numerals. A sign-value system does not need arithmetic numerals because they are made by repetition (except for the Ionic system), and a positional system does not need geometric numerals because they are made by position. However, the spoken language uses both arithmetic and geometric numerals.

In certain areas of computer science, a modified base k positional system is used, called bijective numeration, with digits 1, 2, ..., k (k ≥ 1), and zero being represented by an empty string. This establishes a bijection between the set of all such digit-strings and the set of non-negative integers, avoiding the non-uniqueness caused by leading zeros. Bijective base-k numeration is also called k-adic notation, not to be confused with p-adic numbers. Bijective base 1 is the same as unary.

All known numeral systems developed before the Babylonian numerals are non-positional,^[27] as are many developed later, such as the Roman numerals. The French Cistercian monks created their own numeral system.

Name	Base	Sample	Approx. First Appearance
Proto-cuneiform numerals
Proto-Elamite numerals
Sumerian numerals	10+60		-3100 3,100 BCE
Egyptian numerals	10		-3000 3,000 BCE
Elamite numerals
Indus numerals
Babylonian numerals	10+60		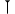-3100 2,000 BCE
Chinese numeralsJapanese numeralsKorean numerals (Sino-Korean) Vietnamese numerals (Sino-Vietnamese)	10	零一二三四五六七八九十百千萬億 (Default, Traditional Chinese) 〇一二三四五六七八九十百千万亿 (Default, Simplified Chinese) 零壹貳參肆伍陸柒捌玖拾佰仟萬億 (Financial, T. Chinese) 零壹贰叁肆伍陆柒捌玖拾佰仟萬億 (Financial, S. Chinese)	-1600 1,600 BCE
Aegean numerals	10	𐄇 𐄈 𐄉 𐄊 𐄋 𐄌 𐄍 𐄎 𐄏  ( ) 𐄐 𐄑 𐄒 𐄓 𐄔 𐄕 𐄖 𐄗 𐄘  ( )𐄙 𐄚 𐄛 𐄜 𐄝 𐄞 𐄟 𐄠 𐄡  ( ) 𐄢 𐄣 𐄤 𐄥 𐄦 𐄧 𐄨 𐄩 𐄪  ( )𐄫 𐄬 𐄭 𐄮 𐄯 𐄰 𐄱 𐄲 𐄳  ( )	-1500 1,500 BCE
Bengali numerals	10	০ ১ ২ ৩ ৪ ৫ ৬ ৭ ৮ ৯	-1400 1,400 BCE
Roman numerals		I V X L C D M	-1000 1,000 BCE
Hebrew numerals	10	(Tatar)	-800 800 BCE
Indian numerals	10	Tamil ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯ ௰ Devanagari ० १ २ ३ ४ ५ ६ ७ ८ ९ Tibetan ༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩	-750 750 – 690 BCE
Greek numerals	10	ō α β γ δ ε ϝ ζ η θ ι ο Αʹ Βʹ Γʹ Δʹ Εʹ Ϛʹ Ζʹ Ηʹ Θʹ	-400 <400 BCE
Phoenician numerals	10	𐤙 𐤘 𐤗 𐤛𐤛𐤛 𐤛𐤛𐤚 𐤛𐤛𐤖 𐤛𐤛 𐤛𐤚 𐤛𐤖 𐤛 𐤚 𐤖 [28]	-25 <250 BCE[29]
Chinese rod numerals	10	𝍠 𝍡 𝍢 𝍣 𝍤 𝍥 𝍦 𝍧 𝍨 𝍩	1 1st Century
Ge'ez numerals	10	፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ ፻	200 3rd – 4th Century15th Century (Modern Style)[30]
Armenian numerals	10	Ա Բ Գ Դ Ե Զ Է Ը Թ Ժ	400 Early 5th Century
Khmer numerals	10	០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩	600 Early 7th Century
Thai numerals	10	๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙	601 7th Century[31]
Abjad numerals	10	غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا	699 <8th Century
Eastern Arabic numerals	10	٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١ ٠	701 8th Century
Vietnamese numerals (Chữ Nôm)	10	𠬠 𠄩 𠀧 𦊚 𠄼 𦒹 𦉱 𠔭 𠃩	799 <9th Century
Western Arabic numerals	10	0 1 2 3 4 5 6 7 8 9	801 9th Century
Glagolitic numerals	10	Ⰰ Ⰱ Ⰲ Ⰳ Ⰴ Ⰵ Ⰶ Ⰷ Ⰸ ...	800 9th Century
Cyrillic numerals	10	а в г д е ѕ з и ѳ і ...	900 10th Century
Rumi numerals	10		900 10th Century
Burmese numerals	10	၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉	1000 11th Century[32]
Tangut numerals	10	Templat:Tangut	1036 11th Century (1036)
Cistercian numerals	10		1200 13th Century
Maya numerals	5+20		1400 <15th Century
Muisca numerals	20		1400 <15th Century
Korean numerals (Hangul)	10	하나 둘 셋 넷 다섯 여섯 일곱 여덟 아홉 열	1443 15th Century (1443)
Aztec numerals	20		1500 16th Century
Sinhala numerals	10	෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯ 𑇡 𑇢 𑇣 𑇤 𑇥 𑇦 𑇧 𑇨 𑇩 𑇪 𑇫 𑇬 𑇭 𑇮 𑇯 𑇰 𑇱 𑇲 𑇳 𑇴	1699 <18th Century
Pentimal runes	10		1800 19th Century
Cherokee numerals	10		1820 19th Century (1820s)
Kaktovik Inupiaq numerals	5+20		1900 20th Century (1994)

Angka nol (bahasa Latin: zephirum, yang berarti kosong atau hampa^[33]) muncul di Mesopotamia sekitar 3 SM.

The first recorded zero appeared in Mesopotamia around 3 B.C.

Peradaban Maya menemukannya secara independen sekitar 4 SM dan dirancang di India pada pertengahan abad ke-5 M.

The Mayans invented it independently circa 4 A.D. It was later devised in India in the mid-fifth century, spread to Cambodia near the end of the seventh century, and into China and the Islamic countries at the end of the eighth. Zero reached western Europe in the 12th century.^[34]

Angka nol tersebut amiug sekitar akhir abad ke-7 M. ??

There was an Indian Hindu mathematician who is said to have first endorsed the number “zero”. Prior to its “official” creation, no other countries used the number until it reached Indian subcontinent.

The first known documented use of zero dates to AD 628, and appeared in the Brāhmasphuṭasiddhānta, the main work of the Indian mathematician Brahmagupta. He treated 0 as a number and discussed operations involving it, including division. By this time (the 7th century) the concept had clearly reached Cambodia as Khmer numerals, and documentation shows the idea later spreading to China and the Islamic world.

Brahmagupta's Brāhmasphuṭasiddhānta is the first book that mentions zero as a number, hence Brahmagupta is usually considered the first to formulate the concept of zero. He gave rules of using zero with negative and positive numbers, such as "zero plus a positive number is a positive number, and a negative number plus zero is the negative number." The Brāhmasphuṭasiddhānta is the earliest known text to treat zero as a number in its own right, rather than as simply a placeholder digit in representing another number as was done by the Babylonians or as a symbol for a lack of quantity as was done by Ptolemy and the Romans.

The use of 0 as a number should be distinguished from its use as a placeholder numeral in place-value systems. Many ancient texts used 0. Babylonian and Egyptian texts used it. Egyptians used the word nfr to denote zero balance in double entry accounting. Indian texts used a Sanskrit word Shunye or shunya to refer to the concept of void. In mathematics texts this word often refers to the number zero.^[35] In a similar vein, Pāṇini (5th century BC) used the null (zero) operator in the Ashtadhyayi, an early example of an algebraic grammar for the Sanskrit language (also see Pingala).

There are other uses of zero before Brahmagupta, though the documentation is not as complete as it is in the Brāhmasphuṭasiddhānta.

Records show that the Ancient Greeks seemed unsure about the status of 0 as a number: they asked themselves "how can 'nothing' be something?" leading to interesting philosophical and, by the Medieval period, religious arguments about the nature and existence of 0 and the vacuum. The paradoxes of Zeno of Elea depend in part on the uncertain interpretation of 0. (The ancient Greeks even questioned whether 1 was a number.)

The late Olmec people of south-central Mexico began to use a symbol for zero, a shell glyph, in the New World, possibly by the 4th century BC but certainly by 40 BC, which became an integral part of Maya numerals and the Maya calendar. Maya arithmetic used base 4 and base 5 written as base 20. George I. Sánchez in 1961 reported a base 4, base 5 "finger" abacus.^{[36][butuh sumber yang lebih baik]}

By 130 AD, Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for 0 (a small circle with a long overbar) within a sexagesimal numeral system otherwise using alphabetic Greek numerals. Because it was used alone, not as just a placeholder, this Hellenistic zero was the first documented use of a true zero in the Old World. In later Byzantine manuscripts of his Syntaxis Mathematica (Almagest), the Hellenistic zero had morphed into the Greek letter Omicron (otherwise meaning 70).

Another true zero was used in tables alongside Roman numerals by 525 (first known use by Dionysius Exiguus), but as a word, nulla meaning nothing, not as a symbol. When division produced 0 as a remainder, nihil, also meaning nothing, was used. These medieval zeros were used by all future medieval computists (calculators of Easter). An isolated use of their initial, N, was used in a table of Roman numerals by Bede or a colleague about 725, a true zero symbol.

Bilangan negatif, pada pertama kali diciptakan oleh Tiongkok dan menggunakan batang merah untuk mewakilinya. Sekitar 630 SM, matematikawan India Brahmagupta menggunakan bilangan positif dan bilangan negatif, masing-masing merepresentasikan aset dan utang.^[37] Pada abad keempat, Diophantus menemukan bilangan negatif yang mengacu pada notasi persamaan ${\displaystyle 4x+20=-4}$ sebagai penyelesaian yang tidak masuk akal, bila solusinya adalah ${\displaystyle x=-4}$ .^[38]

Before any number system was created people used rocks, sticks or counted on their fingers, matematikawan Italia bernama Girolamo Cardano menjelaskan bilangan negatif hanyalah "fiktif" and accepted the possibility of them being useful.

Chinese:

The Chinese are credited with being the first known culture to recognize and use negative numbers. They used red rods to represent negative numbers.

Europe started using negative numbers in 1545.

Before any number system was created people used rocks, sticks or counted on their fingers. There was an Italian mathematician by the name of Girolamo Cardano, who described negative numbers as ‘fictitious’ and accepted the possibility of them being useful.

Negative numbers were finally accepted into the number system in the 19th century. Negative numbers were found to be useful solving tricky equations like cubic and quartic equations.

Although the first set of rules for dealing with negative numbers was stated in the 7th century by the Indian mathematician Brahmagupta, it is surprising that in 1758 the British mathematician Francis Maseres was claiming that negative numbers

"... darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple" .^[39]

For a long time, negative solutions to problems were considered "false". In Hellenistic Egypt, the Greek mathematician Diophantus in the 3rd century AD referred to an equation that was equivalent to 4x + 20 = 4 (which has a negative solution) in Arithmetica, saying that the equation was absurd.^[40] For this reason Greek geometers were able to solve geometrically all forms of the quadratic equation which give positive roots; while they could take no account of others.^[41]

Negative numbers appear for the first time in history in the Nine Chapters on the Mathematical Art (Jiu zhang suan-shu), which in its present form dates from the period of the Han Dynasty (202 BC – AD 220), but may well contain much older material.^[42] The mathematician Liu Hui (c. 3rd century) established rules for the addition and subtraction of negative numbers. The historian Jean-Claude Martzloff theorized that the importance of duality in Chinese natural philosophy made it easier for the Chinese to accept the idea of negative numbers.^[43] The Chinese were able to solve simultaneous equations involving negative numbers. The Nine Chapters used red counting rods to denote positive coefficients and black rods for negative.^[43][44] This system is the exact opposite of contemporary printing of positive and negative numbers in the fields of banking, accounting, and commerce, wherein red numbers denote negative values and black numbers signify positive values. Liu Hui writes:

Now there are two opposite kinds of counting rods for gains and losses, let them be called positive and negative. Red counting rods are positive, black counting rods are negative.^[43]

The ancient Indian Bakhshali Manuscript carried out calculations with negative numbers, using "+" as a negative sign.^[45] The date of the manuscript is uncertain. LV Gurjar dates it no later than the 4th century,^[46] Hoernle dates it between the third and fourth centuries, Ayyangar and Pingree dates it to the 8th or 9th centuries,^[47] and George Gheverghese Joseph dates it to about AD 400 and no later than the early 7th century,^[48]

During the 7th century AD, negative numbers were used in India to represent debts. The Indian mathematician Brahmagupta, in Brahma-Sphuta-Siddhanta (written c. AD 630), discussed the use of negative numbers to produce the general form quadratic formula that remains in use today.^[40] He also found negative solutions of quadratic equations and gave rules regarding operations involving negative numbers and zero, such as "A debt cut off from nothingness becomes a credit; a credit cut off from nothingness becomes a debt." He called positive numbers "fortunes", zero "a cipher", and negative numbers "debts".^[49][50]

In the 9th century, Islamic mathematicians were familiar with negative numbers from the works of Indian mathematicians, but the recognition and use of negative numbers during this period remained timid.^[51] Al-Khwarizmi in his Al-jabr wa'l-muqabala (from which we get the word "algebra") did not use negative numbers or negative coefficients.^[51] But within fifty years, Abu Kamil illustrated the rules of signs for expanding the multiplication ${\displaystyle (a\pm b)(c\pm d)}$ ,^[52] and al-Karaji wrote in his al-Fakhrī that "negative quantities must be counted as terms".^[51] In the 10th century, Abū al-Wafā' al-Būzjānī considered debts as negative numbers in A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen.^[52]

By the 12th century, al-Karaji's successors were to state the general rules of signs and use them to solve polynomial divisions.^[51] As al-Samaw'al writes:

the product of a negative number—al-nāqiṣ—by a positive number—al-zāʾid—is negative, and by a negative number is positive. If we subtract a negative number from a higher negative number, the remainder is their negative difference. The difference remains positive if we subtract a negative number from a lower negative number. If we subtract a negative number from a positive number, the remainder is their positive sum. If we subtract a positive number from an empty power (martaba khāliyya), the remainder is the same negative, and if we subtract a negative number from an empty power, the remainder is the same positive number.^[51]

In the 12th century in India, Bhāskara II gave negative roots for quadratic equations but rejected them because they were inappropriate in the context of the problem. He stated that a negative value is "in this case not to be taken, for it is inadequate; people do not approve of negative roots."

European mathematicians, for the most part, resisted the concept of negative numbers until the middle of the 19th century (!)^[53] In the 18th century it was common practice to ignore any negative results derived from equations, on the assumption that they were meaningless.^[54] In A.D. 1759, Francis Maseres, an English mathematician, wrote that negative numbers "darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple". He came to the conclusion that negative numbers were nonsensical.^[55]

Fibonacci allowed negative solutions in financial problems where they could be interpreted as debits (chapter 13 of Liber Abaci, AD 1202) and later as losses (in Flos). In the 15th century, Nicolas Chuquet, a Frenchman, used negative numbers as exponents^[56] but referred to them as "absurd numbers".^[57] In his 1544 Arithmetica Integra Michael Stifel also dealt with negative numbers, also calling them numeri absurdi. In 1545, Gerolamo Cardano, in his Ars Magna, provided the first satisfactory treatment of negative numbers in Europe.^[40] He did not allow negative numbers in his consideration of cubic equations, so he had to treat, for example, x³ + ax = b separately from x³ = ax + b (with a,b > 0 in both cases). In all, Cardano was driven to the study of thirteen different types of cubic equations, each expressed purely in terms of positive numbers. (Cardano also dealt with complex numbers, but understandably liked them even less.)

en:Number#History

[[en:n-standard_positional_numeral_systems

[[en:List_of_numeral_systems#By_type_of_notation]]

~