Daftar grup kecil

Untuk ${\displaystyle n=1,2,\dots }$ jumlah grup nonisomorfik dari order ${\displaystyle n}$ adalah

1, 1, 1, 2, 1, 2, 1, 5, 2, 2, 1, 5, 1, 2, 1, 14, 1, 5, 1, 5, ... (barisan A000001 pada OEIS)

Untuk grup berlabel, lihat (barisan A034383 pada OEIS).

Setiap grup diberi nama oleh Perpustakaan Grup Kecil sebagai G_oⁱ, di mana o adalah urutan grup, dan i adalah indeks grup dalam urutan itu.

Nama grup umum:

• Z_n: grup siklik dengan urutan n (notasi C_n juga digunakan; itu isomorfik ke grup aditif dari Z/nZ).
• Dih_n: grup dihedral dengan orde 2n (sering kali notasi D_n atau D_2n digunakan)
  • K₄: grup empat Klein dari urutan 4, sama seperti Z₂ × Z₂ dan Dih₂.
• S_n: kelompok simetris derajat n , berisi elemen n ! permutasi dari n .
• A_n: grup alternatif derajat n , yang berisi elemen permutasi genap dari elemen n , dengan urutan 1 untuk n = 0, 1, dan urutan n ! / 2 jika tidak.
• Dic_n atau Q_4n: grup siklik dari urutan 4n .
  • Q₈: grup angka empat dari order 8, juga Dic₂.

Notasi Z_n dan Dih_n memiliki keuntungan bahwa grup titik dalam tiga dimensi C_n dan D_n tidak memiliki notasi yang sama. Ada lebih banyak grup isometri daripada keduanya, dari jenis kelompok abstrak yang sama.

Notasi G × H menunjukkan produk langsung dari dua kelompok; Gⁿ menunjukkan produk langsung dari grup dengan waktu n itu sendiri. G ⋊ H menunjukkan produk semidirect di mana H bekerja pada G ; ini mungkin juga tergantung pada pilihan aksi H pada G .

Abelian dan grup sederhana dicatat. (Untuk grup urutan n < 60, grup sederhana tepatnya adalah grup siklik Z_n, untuk prime n.) Tanda persamaan ("=") menunjukkan isomorfisme.

Elemen identitas dalam grafik siklus diwakili oleh lingkaran hitam. Urutan terendah di mana grafik siklus tidak secara unik mewakili sebuah grup adalah urutan 16.

Dalam daftar subgrup, trivial group dan group itu sendiri tidak terdaftar. Jika ada beberapa subgrup isomorfik, jumlah subgrup tersebut ditunjukkan dalam tanda kurung.

Grup abelian hingga adalah kelompok siklik, atau produk langsungnya; lihat grup abelian.Jumlah grup urutan abelian nonisomorfik ${\displaystyle n=1,2,\dots }$ adalah

1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 1, 2, 1, 1, 1, 5, 1, 2, 1, 2, ... (barisan A000688 pada OEIS)

Untuk kelompok Abelian berlabel, lihat (barisan A034382 pada OEIS).

Daftar semua grup abelian hingga urutan 31

Urutan	ID	Goi	Kelompok	Subgrup yang tepat Nontrivial	Siklus grafik	Sifat
1	1	G11	Z1 = S1 = A2	–		Trivial. Berhubung dgn putaran. Bergantian. Simetris. SD.
2	2	G21	Z2 = S2 = Dih1	–		Sederhana. Simetris. Berhubung dgn putaran. Dasar. (Grup non-trivial terkecil.)
3	3	G31	Z3 = A3	–		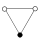Sederhana. Bergantian. Berhubung dgn putaran. Dasar.
4	4	G41	Z4 = Dic1	Z2		Siklik.
	5	G42	Z22 = K4 = Dih2	Z2 (3)		Dasar. Produk. (Klein empat grup. Grup non-siklik terkecil.)
5	6	G51	Z5	–		Sederhana. Siklik. Dasar.
6	8	G62	Z6 = Z3 × Z2[1]	Z3, Z2		Siklik. Produk.
7	9	G71	Z7	–		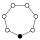Sederhana. Siklik. Dasar.
8	10	G81	Z8	Z4, Z2		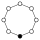Siklik.
	11	G82	Z4 × Z2	Z22, Z4 (2), Z2 (3)		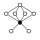Produk.
	14	G85	Z23	Z22 (7), Z2 (7)		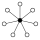Produk. Dasar. (Elemen non-identitas sesuai dengan titik pada bidang Fano, Z2 × Z2 subgrup ke baris.)
9	15	G91	Z9	Z3		Siklik.
	16	G92	Z32	Z3 (4)		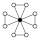Dasar. Produk.
10	18	G102	Z10 = Z5 × Z2	Z5, Z2		Siklik. Produk.
11	19	G111	Z11	–		Sederhana. Siklik. Dasar.
12	21	G122	Z12 = Z4 × Z3	Z6, Z4, Z3, Z2		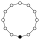Cyclic. Product.
	24	G125	Z6 × Z2 = Z3 × Z22	Z6 (3), Z3, Z2 (3), Z22		Product.
13	25	G131	Z13	–		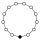Simple. Cyclic. Elementary.
14	27	G142	Z14 = Z7 × Z2	Z7, Z2		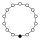Cyclic. Product.
15	28	G151	Z15 = Z5 × Z3	Z5, Z3		Cyclic. Product.
16	29	G161	Z16	Z8, Z4, Z2		Cyclic.
	30	G162	Z42	Z2 (3), Z4 (6), Z22, Z4 × Z2 (3)		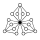Product.
	33	G165	Z8 × Z2	Z2 (3), Z4 (2), Z22, Z8 (2), Z4 × Z2		Product.
	38	G1610	Z4 × Z22	Z2 (7), Z4 (4), Z22 (7), Z23, Z4 × Z2 (6)		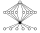Product.
	42	G1614	Z24 = K42	Z2 (15), Z22 (35), Z23 (15)		Product. Elementary.
17	43	G171	Z17	–		Simple. Cyclic. Elementary.
18	45	G182	Z18 = Z9 × Z2	Z9, Z6, Z3, Z2		Cyclic. Product.
	48	G185	Z6 × Z3 = Z32 × Z2	Z6, Z3, Z2		Product.
19	49	G191	Z19	–		Simple. Cyclic. Elementary.
20	51	G202	Z20 = Z5 × Z4	Z10, Z5, Z4, Z2		Cyclic. Product.
	54	G205	Z10 × Z2 = Z5 × Z22	Z5, Z2		Product.
21	56	G212	Z21 = Z7 × Z3	Z7, Z3		Cyclic. Product.
22	58	G222	Z22 = Z11 × Z2	Z11, Z2		Cyclic. Product.
23	59	G231	Z23	–		Simple. Cyclic. Elementary.
24	61	G242	Z24 = Z8 × Z3	Z12, Z8, Z6, Z4, Z3, Z2		Cyclic. Product.
	68	G249	Z12 × Z2 = Z6 × Z4 = Z4 × Z3 × Z2	Z12, Z6, Z4, Z3, Z2		Product.
	74	G2415	Z6 × Z22 = Z3 × Z23	Z6, Z3, Z2		Product.
25	75	G251	Z25	Z5		Cyclic.
	76	G252	Z52	Z5		Product. Elementary.
26	78	G262	Z26 = Z13 × Z2	Z13, Z2		Cyclic. Product.
27	79	G271	Z27	Z9, Z3		Cyclic.
	80	G272	Z9 × Z3	Z9, Z3		Product.
	83	G275	Z33	Z3		Product. Elementary.
28	85	G282	Z28 = Z7 × Z4	Z14, Z7, Z4, Z2		Cyclic. Product.
	87	G284	Z14 × Z2 = Z7 × Z22	Z14, Z7, Z4, Z2		Product.
29	88	G291	Z29	–		Simple. Cyclic. Elementary.
30	92	G304	Z30 = Z15 × Z2 = Z10 × Z3 = Z6 × Z5 = Z5 × Z3 × Z2	Z15, Z10, Z6, Z5, Z3, Z2		Cyclic. Product.
31	93	G311	Z31	–		Simple. Cyclic. Elementary.

Jumlah grup non-abelian, berdasarkan urutan, dihitung dengan (barisan A060689 pada OEIS).Namun, banyak ordo tidak memiliki kelompok non-abelian. Urutan keberadaan grup non-abelian adalah

6, 8, 10, 12, 14, 16, 18, 20, 21, 22, 24, 26, 27, 28, 30, 32, 34, 36, 38, 39, 40, 42, 44, 46, 48, 50, ... (barisan A060652 pada OEIS)

Daftar semua grup nonabelian sampai urutan 31

Urutan	ID	Goi	Kelompok	Subgrup yang tepat Nontrivial	Siklus grafik	Properti
6	7	G61	Dih3 = S3 = D6	Z3, Z2 (3)		Grup dihedral, grup non-abelian terkecil, grup simetris, kelompok Frobenius
8	12	G83	Dih4 = D8	Z4, Z22 (2), Z2 (5)		Grup dihedral. Grup ekstraspesial. Nilpotent.
	13	G84	Q8 = Dic2 = <2,2,2>[butuh klarifikasi]	Z4 (3), Z2		Grup angka empat, grup Hamiltonian. semua subgrup adalah normal tanpa grup abelian. Grup terkecil G yang menunjukkan bahwa untuk subgrup normal H grup hasil bagi G / H tidak perlu isomorfik ke subgrup G . Grup ekstraspesial Grup dihedral biner. Nilpotent.
10	17	G101	Dih5 = D10	Z5, Z2 (5)		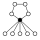Dihedral group, Frobenius group
12	20	G121	Q12 = Dic3 = <3,2,2> = Z3 ⋊ Z4	Z2, Z3, Z4 (3), Z6		Grup dihedral biner
	22	G123	A4 = K4 ⋊ Z3 = (Z2 × Z2) ⋊ Z3	Z22, Z3 (4), Z2 (3)		Grup alternatif. Tidak ada subgrup berorde 6, meskipun 6 membagi urutannya. Grup Frobenius
	23	G124	Dih6 = D12 = Dih3 × Z2	Z6, Dih3 (2), Z22 (3), Z3, Z2 (7)		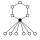Dihedral group, product
14	26	G141	Dih7 = D14	Z7, Z2 (7)		Dihedral group, Frobenius group
16[2]	31	G163	G4,4 = K4 ⋊ Z4 (Z4 × Z2) ⋊ Z2	E8, Z4 × Z2 (2), Z4 (4), K4 (6), Z2 (6)		Has the same number of elements of every order as the Pauli group. Nilpotent.
	32	G164	Z4 ⋊ Z4			The squares of elements do not form a subgroup. Has the same number of elements of every order as Q8 × Z2. Nilpotent.
	34	G166	Z8 ⋊ Z2			Sometimes called the modular group of order 16, though this is misleading as abelian groups and Q8 × Z2 are also modular. Nilpotent.
	35	G167	Dih8 = D16	Z8, Dih4 (2), Z22 (4), Z4, Z2 (9)		Dihedral group. Nilpotent.
	36	G168	QD16		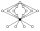	The order 16 quasidihedral group. Nilpotent.
	37	G169	Q16 = Dic4 = <4,2,2>			generalized quaternion group, binary dihedral group. Nilpotent.
	39	G1611	Dih4 × Z2	Dih4 (4), Z4 × Z2, Z23 (2), Z22 (13), Z4 (2), Z2 (11)		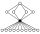Product. Nilpotent.
	40	G1612	Q8 × Z2			Hamiltonian, product. Nilpotent.
	41	G1613	(Z4 × Z2) ⋊ Z2			The Pauli group generated by the Pauli matrices. Nilpotent.
18	44	G181	Dih9 = D18			Dihedral group, Frobenius group
	46	G183	S3 × Z3		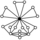	Product
	47	G184	(Z3 × Z3) ⋊ Z2			Frobenius group
20	50	G201	Q20 = Dic5 = <5,2,2>			Binary dihedral group
	52	G203	Z5 ⋊ Z4			Frobenius group
	53	G204	Dih10 = Dih5 × Z2 = D20			Dihedral group, product
21	55	G211	Z7 ⋊ Z3	Z7, Z3 (7)		Smallest non-abelian group of odd order. Frobenius group
22	57	G221	Dih11 = D22	Z11, Z2 (11)		Dihedral group, Frobenius group
24	60	G241	Z3 ⋊ Z8			Central extension of S3
	62	G243	SL(2,3) = 2T = Q8 ⋊ Z3			Binary tetrahedral group
	63	G244	Q24 = Dic6 = <6,2,2> = Z3 ⋊ Q8			Binary dihedral
	64	G245	Z4 × S3			Product
	65	G246	Dih12			Dihedral group
	66	G247	Dic3 × Z2 = Z2 × (Z3 ⋊ Z4)			Product
	67	G248	(Z6 × Z2) ⋊ Z2 = Z3 ⋊ Dih4			Double cover of dihedral group
	69	G2410	Dih4 × Z3			Product. Nilpotent.
	70	G2411	Q8 × Z3			Product. Nilpotent.
	71	G2412	S4	28 proper, non-trivial subgroups. 9 subgroups, combining those that are isomorphic. Subgroups include S2, S3, A3, A4, D8.[3]		Symmetric group. Has no normal Sylow subgroups.
	72	G2413	A4 × Z2			Product
	73	G2414	D12× Z2			Product
26	77	G261	Dih13			Dihedral group, Frobenius group
27	81	G273	Z32 ⋊ Z3			All non-trivial elements have order 3. Extraspecial group. Nilpotent.
	82	G274	Z9 ⋊ Z3			Extraspecial group. Nilpotent.
28	84	G281	Z7 ⋊ Z4			Binary dihedral group
	86	G283	Dih14			Dihedral group, product
30	89	G301	Z5 × S3			Product
	90	G302	Z3 × Dih5			Product
	91	G303	Dih15			Dihedral group, Frobenius group

Kelompok kecil urutan kekuatan utama p ⁿ diberikan sebagai berikut:

• Urutan p : Satu-satunya grup adalah siklik.
• Order p ² : Hanya ada dua grup, keduanya abelian.
• Order p ³ : Ada tiga grup abelian, dan dua grup non-abelian. Salah satu grup non-abelian adalah produk semidirect dari subgrup siklik normal p² oleh grup siklik urutan p . Yang lainnya adalah grup angka empat untuk p = 2 dan segrup eksponen p untuk p > 2.
• Urutan p ⁴ : Klasifikasinya rumit, dan menjadi lebih sulit saat eksponen p meningkat.

Sebagian besar grup orde kecil memiliki subgrup Sylow p P dengan normal komplemen p pada N untuk beberapa bilangan prima p yang membagi urutan, sehingga dapat diklasifikasikan dalam hal kemungkinan bilangan prima p , grup p pada P , grup N , dan tindakan P pada N . Dalam beberapa hal ini mengurangi klasifikasi kelompok ini menjadi klasifikasi grup p . Beberapa kelompok kecil yang tidak memiliki komplemen p normal meliputi.

• Klasifikasi grup sederhana hingga
• Deret komposisi
• Daftar grup sederhana hingga
• Jumlah grup dari pesanan tertentu
• Kotak Latin kecil dan kuasigrup

• Coxeter, H. S. M.; Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.  Parameter |name-list-style= yang tidak diketahui akan diabaikan (bantuan), Table 1, Nonabelian groups order<32.
• Hall, Jr., Marshall; Senior, James K. (1964). "The Groups of Order 2ⁿ (n ≤ 6)". Macmillan. MR 0168631. Katalog dari 340 grup ordo yang membagi 64 dengan tabel hubungan penentu, konstanta, dan kisi subgrup dari setiap grup. 

• Grup tertentu dalam Wiki Properti Grup
• Grup urutan tertentu
• Besche, H. U.; Eick, B.; O'Brien, E. "small group library". Diarsipkan dari versi asli tanggal 2012-03-05.  Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)
• GroupNames database