Уравнение

Неизвестни, решения, тъждествени преобразувания

Следният пример е взет от книгата „Китаб ал-джабр уал-мукабала“ на Мохамед ал-Хорезми, един от основоположниците на алгебрата^[4]

Един човек умрял и оставил поравно наследството си на четиримата си сина като направил дарение на един човек, равно на дела на един от синовете си, и на друг четвърт от разликата между една трета от наследството и първото дарение. Ако с x е означен дела от наследството, който получава всеки един син, задачата се преобразува в следното уравнение, в което стойността 1 вдясно обозначава цялото наследство: $${\displaystyle (1)\quad 4x+x+{\frac {1}{4}}\left({\frac {1}{3}}-x\right)=1}$$

В примера формулираното уравнение означава, че равенството (1) е тъждествено на описаната задача. За да се получи отговора, трябва да се определи единствената стойност на неизвестното x, за която равенството е изпълнено – решение (или корен) на уравнението. Манипулирането на неизвестното дава възможност за решаване на някои уравнения, като представеното тук. Това става чрез преобразуване на уравнението в друго, което е тъждествено на първоначалното.

Две уравнения са тъждествени, ако имат едно и също дефиниционно множество и едни и същи корени. Основните тъждествени преобразувания (начини за получаване на тъждествено на дадено уравнение) са:

• Размяна на двете страни на равенството
• Добавяне към двете страни на равенството на един и същ аритметичен израз, който не стеснява дефиниционното множество
• Умножаване на двете страни на равенството с един и същ аритметичен израз, който е различен от 0 и не стеснява дефиниционното множество (например, умножението с 1/x на уравнение от вида 5x = 0 не е тъждествено преобразование, защото изключва 0 от дефиниционното множество на променливата x)
• Степенуване на двете страни на равенството с една и съща степен, която не стеснява дефиниционното множество

Решаването на уравнението в примера може да стане по следния начин: Опростяване на израза вляво $${\displaystyle {\frac {19}{4}}x+{\frac {1}{12}}=1}$$ Добавяне на -1/12 към двете страни на равенството $${\displaystyle {\frac {19}{4}}x={\frac {11}{12}}}$$ Умножаване с 4/19 на двете страни на равенството $${\displaystyle x={\frac {11}{57}}}$$

Параметри

Параметри в уравненията са променливи, които за разлика от неизвестните могат да присъстват и в решението. Такива уравнения се наричат параметрични и са използвани за пръв път през 16 век от Франсоа Виет като средство за общо решаване на цели групи уравнения,^[5] като тези в следния пример:

Пример за параметрично уравнение^[6]

Търси се броят на реалните корени на следните уравнения: $${\displaystyle (1)\;x^{2}=2x+1,\;(2)\;x^{2}=2x-2\;{\text{и}}\;(3)\;x^{2}=2x-1}$$ Задачата може да се реши, като се въведе функцията f(x), която съпоставя на всяко x стойността x2. Нейната графика е квадратна парабола, показана в синьо на схемата вдясно. Функцията g1(x) съпоставя на x стойността 2.x +1 (червената права). Корените на уравнение (1) са абсцисите на пресечните точки на параболата и червената права, като графичното представяне показва, че съществуват две решения, съответстващи на двете пресечни точки. За решаването на уравнение (2) се въвежда функцията g-2(x), която съпоставя на x стойността 2.x -2 (виолетовата права). Тя не пресича параболата, което означава, че уравнението няма решение. В последния случай се въвежда функцията g-1(x), която съпоставя на x стойността 2.x -1 (зелената права). Нейната графика е права, успоредна на първите две, която има една обща точка с параболата и съответно третото уравнение има едно решение. Задачата може да се реши по по-общ начин, като в уравненията се въведе параметър a, който може да заема произволни стойности, а трите уравнения се разглеждат като частни случаи при стойности на параметъра a 1, -2 и -1: $${\displaystyle (4)\quad x^{2}=2x+a}$$ <

Уравнение (4) се нарича параметрично уравнение, а променливата a – параметър.

Полиномни уравнения

 Основна статия: Полиномно уравнение

Основна категория уравнения, изследвани от алгебрата, са полиномните уравнения, които имат общия вид:

$${\displaystyle P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x+a_{0}=0\!}$$

където a_n ≠ 0, а стойността n се нарича степен на уравнението.

Наличието на добре разработени методи за решаването на полиномни уравнения дава възможност за решаването чрез подходяща замяна на неизвестното и на други групи уравнения. Например, уравнението e^2x – (e^a + e^b)e^x + e^a+b = 0 може да бъде трансформирано в полиномно уравнение от втора степен чрез полагането X = e^x.

Решаването на полиномните уравнения от първите няколко степени е сравнително просто. При уравненията от първа степен (линейни уравнения) решението е:

$${\displaystyle x={\frac {-a_{0}}{a_{1}}}\!}$$

При уравненията от втора степен (квадратни уравнения) корените също може да се получат в явен вид, когато коефициентите и корените са реални числа:

$${\displaystyle x={\frac {-a_{1}\pm {\sqrt {{a_{1}}^{2}-4{a_{2}}{a_{0}}}}}{2{a_{2}}}}}$$

където условието за реалност на корените е стойността под квадратния корен, наричана дискриминанта, да бъде по-голяма или равна на нула.

Решаването на полиномните уравнения от трета степен (кубични уравнения) е по-сложна задача. Италианските математици през Ренесанса установяват, че получаването на общо решение изисква добавянето към множеството на числата на имагинерните числа.^[7] Това откритие дава възможност за формулирането на затворени решения на уравненията от трета и четвърта степен – съответно формула на Кардано и формула на Ферари.

По-късно е изведена и основната теорема на алгебрата, според която всяко полиномно уравнение от степен по-голяма от нула и с реални или комплексни коефициенти има поне един комплексен корен. Макар че тази теорема гарантира съществуването на решение за много широк кръг полиномни уравнения, тя не предлага явно решение, а наличието на комплексни корени на уравненията с реални коефициенти не е интуитивно очевидно. Теоремата на Абел-Руфини дава обяснение на този факт, като показва, че за полиномните уравнения от по-висока степен не съществува обща формула, подобна на тези за уравненията до четвърта степен. Този извод, до който достига Нилс Абел, е допълнен от Еварист Галоа, който извежда необходимото и достатъчно условие за наличие на решение от подобен вид на полиномните уравнения. В историята на математиката основната теорема на алгебрата и теоремата на Абел-Руфини образуват популярната през 19 век теория на уравненията, която днес не се разглежда като самостоятелна област на математиката.

Системи линейни уравнения

 Основна статия: Система линейни уравнения

Друга група уравнения, изследвани от алгебрата, са векторните линейни уравнения от вида:

$${\displaystyle a(x)+b=0\!}$$

където a е линейно изображение на векторното пространство E във векторното пространство F, b е вектор от пространството F, а x е променлива, дефинирана в пространството E.

Ако пространствата E и F са с крайна размерност, съответно n и m, изборът на база на E и F дава възможност изображението a да се представи под формата на матрица (a_jk), x – под формата на вектор стълб с n координати (x_k) и b – като вектор стълб с m координати (b_j). Така векторното линейно уравнение може да бъде записано като система от линейни уравнения:

$${\displaystyle \quad \left\{{\begin{matrix}a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+...+a_{mn}x_{n}=b_{m}\end{matrix}}\right.}$$

Системите линейни уравнения намират широко приложение в науката и техниката, често в методи за приблизително решаване на диференциални уравнения, поради което съществуват множество методи за тяхното решаване. В случая, когато размерностите n и m са равни и детерминантата на матрицата a е различна от нула, решението на системата може да бъде получено в явен вид чрез метода на Крамер. Този начин за решаване на системите е неефективен и в практиката по-често се използват итерационни алгоритми, като метода на Гаус.^[8] Неговата цел е да отдели отделните неизвестни, като чрез поредица тъждествени преобразувания получи линейни уравнения с едно неизвестно. Методът на Гаус е известен още през Древността. Негов вариант е описан в Глава 8 на китайската математическа книга от 2 век пр.н.е. „Дзиуджан Суаншу“.^[9]

Геометрична интерпретация на линейните уравнения

Геометричната интерпретация на системите линейни уравнения дава допълнителна информация за техния характер. Изображението на линейния оператор a образува векторно подпространство, подобно на равнината в триизмерното пространство. Ядрото на a (векторите от дефиниционното множество, чието изображение е нулевият вектор) също е подпространство. Тези резултати показват, че множестовото от решенията образува афинно пространство.

Този подход дава възможност за създаване на алгоритми за решение, които отчитат характерните особености на a. В някои частни случаи съществуват методи, позволяващи по-бързото намиране на решение, отколкото чрез метода на Гаус. Например, възможно е да не се търси пряко решение на уравнението a.x + b = 0, а да се отговори на друг въпрос, привидно по-сложен – да се намери екстремума на f(x), дефинирана като:

$${\displaystyle \forall x\in E\quad f(x)={\frac {1}{2}}\langle ax,x\rangle +\langle b,x\rangle }$$

Този екстремум е и решението на системата линейни уравнения. За да се разбере методът на решение, най-просто е да се разгледа случаят с две измерения – графиката на f има овална форма, както е показано на схемата вляво. Ако се тръгне от произволна точка x₀ и се следва кривата с най-голям наклон (показана като червена парабола на схемата вляво и като червена отсечка на схемата вдясно), най-високата точка се означава като x₁. От точка x₁ отново се следва кривата с най-голям наклон, показана в зелено на схемите. Този алгоритъм се нарича метод на най-бързото изкачване. Ако вместо да се следва точно пътя на най-големия наклон, се избере посока, ортогонална на предходните посоки, методът дава решение за максимум n стъпки, където n е броят на измеренията на E.

Аналитична геометрия

 Основна статия: Аналитична геометрия

В евклидовата геометрия е възможно всяка точка от пространството да се съпоставят определени координати, например чрез използването на ортонормален базис. Този подход дава възможност геометричните фигури да бъдат описвани с помощта на уравнения. Така например, равнина в триизмерното пространство може да се опише като съвкупността от решенията на уравнение от вида a.x + b.y + c.z + d = 0, където a, b, c и d са реални числа, а неизвестните x, y и z са координатите на точките от равнината в избраната координатна система. Числата a, b и c са координати на вектор, перпендикулярен на описваната от уравнението равнина. Правата се дефинира като сечение на две равнини и може да се опише като съвкупността от решенията на линейно уравнение със стойности в ℝ² или на система от две линейни уравнения със стойности в ℝ, където ℝ е множеството на реалните числа.

Коничните сечения представляват сечения на конус с уравнение x² + y² = z² и равнина – в пространството всяко конично сечение се дефинира като множеството от точки, чиито координати са решения на уравнение на равнина и на посоченото уравнение. Тази форма дава възможност да се определи положението и свойствата на фокусите на коничните сечения.

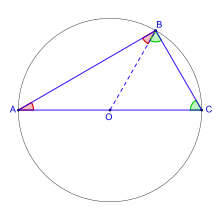
С използването на този подход могат да се получат и уравнения, чиято цел не е изразяването на решения, подобни на току-що описаните. Пример за това е теоремата на Талес, според която един триъгълник е правоъгълен, ако една от страните му е диаметър на описаната около него окръжност. При подходящ избор на правоъгълна координатна система уравнението на окръжността може да се опише като: x² + y² = 1, а точките A и C на схемата вдясно имат координати съответно (-1,0) и (1,0). Ако AB е перпендикулярна на CB, съответните вектори също трябва да са ортогонални. Така с помощта на уравнението на окръжността е лесно да се покаже верността на теоремата:

$${\displaystyle {\overrightarrow {AB}}\cdot {\overrightarrow {CB}}=\langle (x-1,y),(x+1,y)\rangle =(x+1)(x-1)+y^{2}=x^{2}+y^{2}-1=0\quad {\text{тъй като}}\quad x^{2}+y^{2}=1}$$

Използването на уравнения дава нови възможности за разрешаване на геометрични задачи. С превръщането на геометричните фигури в уравнения декартовата координатна система преобразува геометричната задача в аналитична, откъдето идва и наименованието на цялата математическа дисциплина – аналитична геометрия. Този подход, демонстриран от Рене Декарт, обогатява и напълно преобразява известната от Античността геометрия.

В наши дни аналитичната геометрия е активно развиващ се клон на математиката. В нейната основа продължава да бъде използването на уравнения за описване на геометрични обекти, но тя прилага и по-сложни методи, базирани на функционалния анализ и линейната алгебра.

Декартови и параметрични уравнения

Представянето на геометрични фигури като уравнения обикновено става по един от два основни метода. При първия се използва уравнение от вида f(x) = 0, където f е функция от евклидовото пространство E с размерност n в ℝ^d, а d е естествено число, по-малко от n. Ако f е достатъчно правилна функция, n – d е размерността на геометричната фигура – ако тя е 1, фигурата е крива, при 2 тя е повърхнина и т.н. Такова уравнение може да се представи и като система от d уравнения с реални корени. Този вид уравнения се наричат декартови, ако x е представено чрез координати в декартова координатна система. Всички уравнения в предходния раздел са декартови.

Другият често използван метод се състои в описването на геометричните фигури с помощта на функция f от ℝ^d в E по такъв начин, че една точка m в E е елемент на фигурата, когато съществува точка x в дефиниционното множество на функцията f, за която f(x) е равно на m. В този случай и при достатъчна правилност на f описаната фигура има размерност d, а уравнението се нарича параметрично. Например, единичната окръжност може да се опише с параметъра θ и параметричните уравнения:

$${\displaystyle \left\{{\begin{matrix}x&=&\cos \theta \\y&=&\sin \theta \end{matrix}}\right.}$$

Ако описваната фигура е достатъчно правилна, например, ако поне локално съответства на дадено многообразие, то е възможно тя да се параметризира. В този контекст локално означава, че ако m е елемент на фигурата, съществува функция f и околност V на точка от дефиниционното множество f, такава че изображението на f остава част от фигурата и такова че изображението на V от f е околност на m във фигурата.

Диофантови уравнения

 Основна статия: Диофантово уравнение

В исторически план първите формализирани уравнения имат аритметичен характер и датират от 3 век.^[10] Ако решението на дадено уравнение се търси не като произволно число, а като цяло число, и ако уравнението е с цели коефициенти, то се нарича диофантово.^[11] Описаните по-горе методи по принцип не са достатъчни за решаването на тази група уравнения, за сметка на това са изключително полезни методите на аритметиката. Относително прост пример е линейното диофантово уравнение с две неизвестни a.x + b.y = c.

С увеличаването на степента на диофантовото уравнение решаването му става далеч по-сложно. Дори уравнението от втора степен далеч не е просто в общия случай (вижте например Теорема на Ферма-Ойлер или Уравнение на Пел). Чрез използването на специално създадени за тази цел методи и предпоставки, като метода на безкрайното спускане и малката теорема на Ферма, става възможно да се решат някои частни случаи.

Общото решение на уравнението от втора степен изисква използването на по-сложни методи, като тези на алгебричната теория на числата. Необходими са по-детайлни представи за числовите множества и изследване на крайни полета и цели алгебрични числа с помощта на теорията на Галоа. Така докато решение на алгебричното уравнение от втора степен е намерено от Хорезми още през 8 век, аналогичното диофантово уравнение е решено едва в края на 19 век от Давид Хилберт. Анализът на диофантовите уравнения често е толкова сложен, че се ограничава до определянето на съществуването на решения и техния брой.

Диофантовите уравнения намират широко приложение в областта на информатиката. Инструменти, основани на техния анализ, дават възможност за откриване и поправяне на грешки и са в основата на алгоритмите на криптологията. В основата на много шифри стоят диофантови уравнения, които се описват просто, но чието решаване изисква практически недостижимо време за обработка. Например, уравнението n = x.y, където n е фиксирано естествено число, а x и y са неизвестните, не може да се реши практически, ако n е произведение на две достатъчно големи прости числа. Това уравнение е основата на популярния алгоритъм за шифриране RSA.^[12]

Алгебрични и трансценденти числа

 Основни статии: Алгебрично число и Трансцендентно число

Алгебрично число е число, което е решение на ненулево полиномно уравнение с една променлива и рационални коефициенти (или еквивалентно – чрез изчистване на знаменатели – с целочислени коефициенти). Числа като пи, които не са алгебрични, се казва, че са трансцендентни. Почти всички реални и комплексни числа са трансцендентни.

Алгебрична геометрия

 Основна статия: Алгебрична геометрия

Алгебраичната геометрия е клон на математиката, изучаващ решенията на полиномни уравнения. Съвременната алгебраична геометрия се основава на по-абстрактни техники на абстрактната алгебра, особено на комутативната алгебра, с езика и проблемите на геометрията.

Основните обекти на изследване в алгебраичната геометрия са алгебраични разновидности, които са геометрични прояви на решения на системи от полиномични уравнения. Примери за най-изследваните класове на алгебрични разновидности са: равнинни алгебрични криви, които включват линии, кръгове, параболи, елипси, хиперболи, кубични криви като елиптични криви, и криви от четвърта степен като лемнискати и овали на Касини. Точка в равнината принадлежи на алгебраична крива, ако нейните координати удовлетворяват дадено полиномно уравнение. Основните въпроси на алгебричната геометрия включват изследване на точките от особен интерес като сингуларни точки, инфлексни точки и безкрайно отдалечени точки. По-сложните въпроси включват топологията на кривата и отношенията между кривите, дадени от различни уравнения.