Equació

Definició - equació, desconeguda i solució

L'exemple següent s'ha tret^[4] del llibre de Muhàmmad ibn Mussa al-Khwarazmí, un dels fundadors de l'àlgebra:

« Un home mor i deixa quatre fills i fa una donació a un home igual a la part d'un dels seus fills i a un altre el quart del que queda. Si x designa la incògnita, aquí la fracció de l'herència que rep cada un dels fills, la pregunta es tradueix en l'equació següent, on el valor 1 a la dreta designa l'herència:${\displaystyle (1)\quad 4x+x+{\frac {1}{4}}(1-x)=1}$ »

En l'exemple, la formulació en forma d'equació, és a dir, la igualtat (1), és equivalent a la pregunta plantejada. Respondre-la significa determinar l'únic valor que ha de prendre la incògnita x perquè la igualtat que defineix l'equació sigui verdadera. El maneig de la incògnita permet resoldre algunes equacions, com la que es presenta aquí. Aquesta visió és font d'una altra manera de definir una equació. Per a l'Enciclopèdia soviètica de matemàtiques, una equació és la traducció, sota una forma analítica, d'un problema.^[5][6] L'equació f(x) = g(x) correspon a la pregunta: per a quin valor de x, l'equació es transforma en igualtat? Aquesta definició descriu bé les primeres equacions estudiades, que són de vegades la formulació matemàtica d'una pregunta de la vida corrent.

Aquesta definició fundada en una pregunta no és la més general: en geometria, l'equació de la circumferència no fa referència a una pregunta.^[7] Tanmateix, la forma continua sent la mateixa: una igualtat entre dues expressions, utilitzant dues variables generalment notades x i y.

Paràmetre

Al segle xvi, Viète, un matemàtic francès, troba un mètode per expressar de manera genèrica una família d'equacions.^[8] Per comprendre'n l'interès, s'il·lustra amb un exemple:

Exemple d'equació paramètrica.

Quin és el nombre de solucions reals[9] de les equacions següents? ${\displaystyle (1)\;x^{2}=2x+1,\;(2)\;x^{2}=2x-2\;{\text{i}}\;(3)\;x^{2}=2x-1}$ Per trobar aquest nombre, es considera la funció f(x), que a x li associa x², la gràfica de la qual és la paràbola representada a la recta en blau. La funció g1(x) associa a x el valor 2·x +1 (la recta vermella). Les solucions de l'equació són les abscisses de les interseccions de la paràbola amb la recta vermella, la representació gràfica mostra l'existència de dues solucions, ja que existeixen dues interseccions. Per a l'equació (2), es considera la funció g-2(x) que a x li associa 2·x -2 (la recta violeta). No troba la paràbola i l'equació no admet solució. Per tractar l'últim cas, es considera la funció g-1(x) que a x li associa 2·x -1 (la recta verda), és una recta paral·lela a la precedent i aquesta vegada existeix una única solució. Una manera global de resoldre aquestes tres qüestions és fer servir una lletra a que representa un nombre qualsevol. Les tres equacions precedents corresponen a la següent, si a és igual a 1, -2 o a -1: ${\displaystyle (4)\quad x^{2}=2x+a}$

L'equació (4) anterior s'anomena equació paramètrica i la lletra a designa el paràmetre. El seu ús permet estudiar les equacions per famílies.

Qüestions que sorgeixen a partir d'una equació

Les qüestions que sorgeixen en l'estudi d'una equació depenen de la seva naturalesa. En la imatge de l'equació precedent, algunes es defineixen amb l'ajuda d'una funció f : R → R, és a dir, del conjunt dels nombres reals en si mateix. L'equació s'escriu f(x) = 0. De vegades, es comença l'estudi per establir l'existència o no de solució a l'equació. El nombre de solucions ve donat per l'estudi de la funció f, aquest cas s'estudia en el paràgraf sobre els zeros d'una funció.

De vegades, és més simple començar per estudiar les propietats de la o de les eventuals solucions, sense preocupar-se per la seva existència. És el cas del problema isoperimètric del triangle. El problema consisteix a trobar el triangle de perímetre donat (es pren aquí el valor 3) de major àrea possible. Si T designa la desconeguda, aquí un triangle de perímetre 3, S(T) la funció que a un triangle li associa la seva àrea i m la fita superior de les superfícies dels triangles de perímetre 3, la traducció en forma d'equació del problema s'escriu:

${\displaystyle S(T)=m\;}$

Des de l'antiguitat, els matemàtics saben que l'única resposta possible és el triangle equilàter.^[10] En canvi, establir l'existència d'una solució és un problema més tècnic i fa ús d'eines desconegudes fins al segle xviii.^{[Nota 4]} L'existència d'una solució està íntimament vinculada al conjunt en el qual se cerca aquesta solució. Si, en l'exemple escollit, aquest conjunt s'estén al dels polígons de perímetre 3, l'equació ja no admet solució. Per establir aquest resultat, es demostra al principi que una eventual solució seria necessàriament un polígon regular.^{[Nota 5]} Ara bé, a mesura que el nombre de costats d'un polígon regular de perímetre donat augmenta, la seva àrea creix més; la qual cosa demostra l'absència de solució, ja que cap polígon regular no és d'àrea màxima.

La forma d'una solució depèn de les necessitats. Agafem, com a exemple, l'equació que defineix el nombre d'or φ: X² - X - 1 = 0. Per a un arquitecte, la forma més pragmàtica és una aproximació decimal com 1,618. En canvi, si l'objectiu és d'establir la fórmula que enllaça la successió de Fibonacci (u_n) ambφ:

${\displaystyle \forall n\in \mathbb {N} \quad u_{n}={\frac {1}{\sqrt {5}}}\left(\varphi ^{n}-(1-\varphi )^{n}\right)}$

és indispensable una forma exacta com (1+ √5)/2. Com que el nombre d'or és irracional, no hi pot haver cap expressió exacta sense l'ajuda d'una funció auxiliar com l'arrel quadrada, ja que les quatre operacions i els nombres enters no permeten expressar més que racionals. L'aproximació de solucions és objecte de vastos estudis, que entren en un àmbit de les matemàtiques anomenat càlcul numèric.^[11]

Teoria d'equacions

La primera teoria d'equacions no fa referència més que a les equacions polinòmiques, és a dir, de la forma P(X) = 0, en què P és un polinomi.^[12] Es basa a fer transformacions als membres de l'equació aplicant les cinc operacions «clàssiques» (addició, multiplicació, subtracció, divisió i extracció d'arrels), tant als coeficients de l'equació com a la seva incògnita.

Si el grau del polinomi és igual a 2 i si els coeficients i les solucions cercades són reals, llavors aquests mètodes permeten trobar les solucions, anomenades arrels, tal com varen descobrir els matemàtics catalans a l'edat mitjana (vegeu l'article Equació de segon grau). L'ús de la tècnica del canvi de variable permet estendre la família d'equacions que es resolen, així, com il·lustra l'exemple^{[Nota 6]} e^2x - (e^a + e^b)e^x + e^a+b = 0, es resol posant X = e^x. Aquest mètode de canvi de variable no es limita a les equacions algebraiques.

Per anar més lluny i resoldre l'equació cúbica, és a dir, de tercer grau, els matemàtics italians del Renaixement varen descobrir la necessitat d'enriquir el conjunt dels nombres afegint-los els nombres imaginaris.^[13] Aquest descobriment permet la resolució de les equacions de tercer i quart grau (vegeu els mètodes de Cardan i Ferrari).

El teorema fonamental de l'àlgebra estableix que tot polinomi de grau superior o igual a 1 i amb coeficients reals o complexos, admet pel cap baix una arrel complexa.^[14] Si bé aquest teorema assegura, en un cas molt general, l'existència d'una solució, no n'ofereix cap formulació explícita. El següent teorema, anomenat teorema d'Abel, n'explica la raó: no existeix, en general, cap fórmula anàloga^{[Nota 7]} a les que hi ha per a equacions de grups més petits o iguals a quatre, capaç d'expressar les arrels. Aquest resultat, obra de Niels Abel,^[15] va ser completat per Évariste Galois, que indica una condició necessària i suficient per a determinar en quins casos les arrels d'una equació polinòmica contenen una expressió d'aquesta natura.^[16] La seva demostració fa servir la teoria de Galois.

Els dos teoremes precedents clouen la teoria d'equacions. Aquesta expressió encara era vigent en matemàtiques durant tot el segle xix.^[17] Es manté en història de les ciències.^[18] Encara es fa servir en matemàtiques,^[19] però s'ha fet rara i una mica passada de moda.

Sistema d'equacions lineals

Una altra família d'equacions que es tracta en àlgebra és la de les equacions lineals. Són les equacions de la forma (1) a(x) + b = 0, en què a és una aplicació lineal d'un espai vectorial E en un espai vectorial F, b un vector de F i x una variable que pertany al conjunt E. Si els espais E i F són de dimensió finita, notats n per a E i m per a F, la tria d'una base d'E i de F permet expressar a en forma d'una matriu (a_jk), x en forma d'un vector columna amb n coordenades (x_k) i b la d'un vector columna amb m coordenades (b_j):

${\displaystyle \left({\begin{matrix}b_{1}\\b_{2}\\\vdots \\b_{m}\\\end{matrix}}\right)=\left({\begin{matrix}a_{11}&a_{12}&...&a_{1n}\\a_{21}&a_{22}&...&a_{2n}\\\vdots &\vdots &\vdots &\vdots \\a_{m1}&a_{m2}&...&a_{mn}\\\end{matrix}}\right)\cdot \left({\begin{matrix}x_{1}\\x_{2}\\\vdots \\x_{n}\\\end{matrix}}\right)}$

o, cosa que és el mateix,

${\displaystyle (2)\quad \left\{{\begin{matrix}a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+...+a_{mn}x_{n}=b_{m}\end{matrix}}\right.}$

D'una equació (1) es passa a un sistema (2) de m equacions amb n desconegudes. Aquesta tècnica, consistent a passar d'una equació vectorial a un sistema de diverses equacions reals de diverses variables reals, no es limita al cas lineal.

Sota la forma (2), hi ha diversos algorismes que permeten trobar una arrel. Si n és igual a m i si el determinant de la matriu a és no nul, és possible fer servir la regla de Cramer. No és l'algorisme més eficient, el mètode del pivot és més simple i més ràpid. Significa aïllar els no variables amb l'ajuda d'una continuació de substitucions. Aquest mètode és antic; se'n troba un d'equivalent al capítol 8 del llibre xinès de matemàtiques titulat Els nou capítols de les arts matemàtiques (九章算术) i datat d'abans de la nostra era.^[20][21] Al segle xiii, Qin Jiushao va anar-hi més lluny i va trobar com resoldre un sistema lineal amb congruències com a coeficients, per resoldre una qüestió vinculada a un «programa de repartiment de grans».^[22]

Equació lineal i geometria

L'enfocament geomètric de l'equació lineal ofereix informacions d'una altra naturalesa. La imatge d'una aplicació lineal a, és a dir, el conjunt dels vectors que són imatge d'algun vector per f forma un subespai vectorial, com ho és un pla en un espai de dimensió tres. El nucli de a, és a dir, els vectors del conjunt de sortida que tenen per imatge el vector nul, és també un subespai. Aquests resultats mostren que el conjunt de les solucions forma un espai afí de direcció al nucli de a.

El punt de vista geomètric permet elaborar algorismes de resolució que tenen en compte les especificitats de a. En certs casos particulars, existeixen tècniques que permeten trobar-hi una solució més ràpidament que amb el mètode del pivot. Un exemple en correspon al cas en què E és un espai euclidià igual a F i a és tal que l'aplicació que a x i y els hi associa <-ax,y> sigui un producte escalar. Aquí, els claudàtors designen el producte escalar inicial de l'espai E.^{[Nota 8]} Això implica que la matriu de a és de determinant no nul i simètrica, si la base de E s'escull ortonormal.

Un mètode consisteix a no intentar resoldre directament l'equació a·x + b = 0, sinó respondre a una altra qüestió, d'aparença més complexa. Es tracta de trobar el punt òptim^{[Nota 9]} de l'expressió que a x li associa f(x), definit per:

${\displaystyle \forall x\in E\quad f(x)={\frac {1}{2}}\langle ax,x\rangle +\langle b,x\rangle }$

El seu punt òptim és la solució de l'equació lineal. Per a comprendre el mètode de resolució, el més simple és de representar el cas en què F és de dimensió 2. Llavors, la gràfica de f té la forma d'un cim, com s'il·lustra a la figura de l'esquerra. Un mètode consisteix a començar en un punt qualsevol x₀ i a seguir la recta de major pendent, il·lustrat en vermell a les figures i que correspon a una paràbola a l'esquerra i a un segment a la dreta. El cim d'aquesta paràbola s'anota com a x₁. A partir del punt x₁, se segueix de nou la recta de major pendent, en verd sobre les figures. Aquesta tècnica porta el nom de descens del gradient.^[23]

Si, en comptes de seguir exactament el camí de major pendent, se n'escull un de direcció ortogonal en les direccions precedents per al producte escalar <-a·x,y>, el mètode convergeix cap a la solució en un màxim de n etapes, si n designa la dimensió de E. Aquest mètode s'anomena el mètode del gradient conjugat.^[24]

Geometria analítica

En geometria euclidiana, és possible associar a cada punt de l'espai un conjunt de coordenades; per exemple, amb l'ajuda d'un sistema de referència ortonormal. Aquest mètode permet caracteritzar figures geomètriques amb l'ajuda d'equacions. Un pla en un espai de dimensió 3 s'expressa com el conjunt de les solucions d'una equació del tipus a·x + b·y + c·z + d = 0, en què a, b, c i d són nombres reals, i x, y, z les incògnites que corresponen a les coordenades d'un punt del pla en la referència ortonormal. Els valors a, b i c són les coordenades d'un vector perpendicular al pla definit per l'equació. Una recta s'expressa com la intersecció de dos plans; és a dir, com les solucions d'una equació lineal amb valors a R² o com les solucions d'un sistema de dues equacions lineals amb valors a R, si R designa el conjunt dels nombres reals.

Una cònica és la intersecció d'un con d'equació x² + y² = z² i d'un pla. En altres paraules, en l'espai, tota cònica és definida com els punts les coordenades dels quals són solucions de l'equació d'un pla en R² i de l'equació precedent. Aquest formalisme permet determinar les posicions i les propietats dels focus de la cònica.

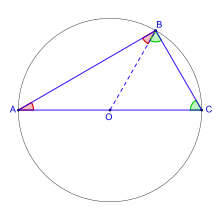
Amb aquest enfocament, s'obtenen equacions l'objectiu de les quals no és l'expressió de les solucions en el sentit del paràgraf precedent. Un exemple en ve donat pel segon teorema de Tales, que indica que un triangle és rectangle si té un costat igual a un diàmetre d'una circumferència i un vèrtex oposat que pertany a la circumferència. Aquest teorema s'il·lustra a la figura de la dreta. Si el sistema de referència s'escull adequadament, l'equació de la circumferència s'escriu: x² + y² = 1, els punts A i C de la figura de la dreta tenen per coordenades respectives (-1,0) i (1,0). Dir que AB és perpendicular a CB vol dir que els vectors associats són ortogonals. L'equació de la circumferència permet concloure la demostració, en efecte:

${\displaystyle {\begin{aligned}{\overrightarrow {AB}}\cdot {\overrightarrow {CB}}&=\langle (x-1,y),(x+1,y)\rangle \\&=(x+1)(x-1)+y^{2}=x^{2}+y^{2}-1=0\quad {\text{ja que}}\quad x^{2}+y^{2}=1\end{aligned}}}$ ^{[Nota 10]}

L'ús d'una equació permet fer servir una nova àrea de les matemàtiques per a resoldre qüestions de geometria. El sistema de referència cartesià transforma un problema de geometria en un problema d'anàlisi, una vegada les figures estudiades s'han traduït en equacions; d'on li ve el nom de geometria analítica.^[25] Aquest punt de vista, descobert per Descartes, va enriquir i modificar la geometria tal com la concebien els matemàtics de la Grècia antiga.^{[Nota 11]}

Actualment, la geometria analítica designa una branca de les matemàtiques en què la recerca és activa. Si bé fa servir sempre l'equació per a caracteritzar una figura, també fa servir eines sofisticades procedents de l'anàlisi funcional o de l'àlgebra lineal.^[26]

Equació cartesiana i paramètrica

Existeixen almenys dos mètodes per a descriure una figura geomètrica amb l'ajuda d'equacions. La primera consisteix a descriure-la per una equació de la forma f(x) = 0, en què f és una funció de l'espai euclidià E de dimensió n en R^d en què d és un enter més petit que n. Si f és una funció prou regular, n - d és la dimensió de la figura geomètrica. Si és igual a 1, la figura és una corba, si és 2, es parla de superfície, etc.^[27] Tal equació es pot escriure també com un sistema de d equacions amb valors en els reals exactament com per al cas de l'equació lineal. Aquest tipus d'equació s'anomena cartesiana si x s'expressa amb l'ajuda de les seves coordenades en un sistema de referència cartesià.^[28] Les equacions descrites en el paràgraf precedent són totes cartesianes, com en la de la circumferència d'equació x² + y² = 1.

Un altre mètode consisteix a descriure la figura geomètrica amb l'ajuda d'una funció f de R^d en E de la manera següent: un punt m de E és element de la figura quan existeix un punt x del conjunt de definició de la funció f tal que f(x) és igual a m. En aquest cas, i depenent d'una regularitat suficient de f (n'hi ha prou que el seu diferencial sigui injectiu), la figura és de dimensió d. Es parla d'equació paramètrica de la figura geomètrica;^[29] aquesta definició de l'equació està relativament allunyada d'aquella que es troba en àlgebra.

Exemple

La circumferència goniomètrica del pla euclidià per equació paramètrica de paràmetre θ:

${\displaystyle \left\{{\begin{matrix}x&=&\cos \theta \\y&=&\sin \theta \end{matrix}}\right.}$

Si la figura és prou regular; per exemple, si correspon a una varietat, almenys localment, existeix una parametrització de la figura. Localment, significa que si m és un element de la figura, existeix una funció f i un veïnat V d'un punt del conjunt de sortida de f tal que la imatge de f quedi inclosa en la figura i tal que la imatge de V per f sigui un veïnat de m en la figura.^[30] Per tant, localment és possible definir la figura amb l'ajuda d'una equació cartesiana.

Equació diofàntica

Històricament, les primeres equacions que es formalitzen són de naturalesa aritmètica i daten del segle iii.^[31] Si se cerca com a solució d'una equació, no un nombre qualsevol, sinó un nombre enter i si l'equació és de coeficients enters, es parla d'equació diofàntica.^[32] Els mètodes descrits anteriorment, generalment, són insuficients per a resoldre les equacions diofàntiques; per fer-ho, són indispensables les eines procedents de l'aritmètica, o almenys de l'aritmètica elemental. Un exemple relativament simple^[33] n'és l'equació lineal amb dues desconegudes a.x + b.y = c.

Si el grau de l'equació augmenta, la qüestió es fa molt més complexa. Ni tan sols una equació de grau 2, en general, no és simple (vegeu per exemple el teorema dels dos quadrats de Fermat o l'equació de Pell-Fermat). A condició d'afegir altres mètodes, com el del descens infinit i nous resultats com el petit teorema de Fermat, és possible resoldre'n alguns casos particulars. El cas general de l'equació de grau 2 demana l'ús d'eines més sofisticades, com les de la teoria algebraica de nombres. Els conjunts de nombres s'enriqueixen, es fan servir els cossos finits i els enters algebraics, que s'estudien, com per a l'equació algebraica, amb l'ajuda de la teoria de Galois. Si bé l'equació algebraica de grau 2 va ser essencialment resolta per Muhàmmad ibn Mussa al-Khwarazmí, un matemàtic àrab del segle viii, i Savasorda, un matemàtic català del segle xii, en va donar la solució completa, cal esperar la fi del segle xix perquè David Hilbert obtingui el seu equivalent diofàntic.^{[Nota 12]} L'estudi de les equacions diofàntiques, sovint, és prou complex per a limitar-lo a establir l'existència de solucions i, si n'existeixen, a determinar-ne el nombre.

Un vast àmbit d'aplicació de les equacions diofàntiques és la informàtica. Les eines procedents dels seus estudis permeten dissenyar codis correctors i són la base d'algorismes de criptografia. Hi ha equacions diofàntiques que s'escriuen de manera simple, però que demanen temps de tractament prohibitius per resoldre-les, són la base dels codis secrets. Per exemple, l'equació n = x·y, en què n és un nombre natural fixat i en què x i y són les desconegudes, no és resoluble en la pràctica, si n és el producte de dos nombres primers prou grans. Aquesta equació és la base del codi RSA.^[34]

Nombre algebraic i transcendent

En lloc de preguntar-se quins nombres són solucions d'una equació donada, es pot considerar el problema invers: de quines equacions un nombre donat n'és solució? Un nombre s'anomena racional si és solució d'una equació de primer grau amb coeficients enters. S'anomena algebraic si és solució d'una equació polinòmica amb coeficients enters. Si no és algebraic, s'anomena transcendent. Així, per a un nombre donat, l'objectiu és trobar les eventuals equacions polinòmiques de les quals aquest nombre és arrel (vegeu l'article Polinomi mínim d'un nombre algebraic).

Per exemple, per a la √2, es planteja la qüestió de saber si és possible construir una equació de primer grau que tingui aquest valor per arrel. Es resol fàcilment: si existeix tal equació, se'n dedueix l'expressió 2·a² = b², en què a i b són nombres naturals. L'anàlisi de la descomposició en factors primers mostra que el terme de la dreta conté el factor 2, un nombre parell de vegades i el de l'esquerra un nombre senar. Aquesta observació demostra que √2 no és un nombre racional.^{[Nota 13]} En canvi, és per definició algebraic, ja que és solució de l'equació X² - 2 = 0.

La mateixa qüestió per al nombre π és més delicada. Per a demostrar que aquest nombre no és solució de cap equació de primer grau amb coeficients en els nombres enters, es fan servir fraccions contínues. Les tècniques són més sofisticades que les que es fan servir per a demostrar la irracionalitat de √2. Mentre que la irracionalitat de √2 ja era coneguda en temps d'Euclides,^[35] cal esperar fins al segle xviii per establir la irracionalitat de π.^[36]

Si demostrar que π no és solució d'una equació del primer grau amb coeficients en els enters no és ja tan simple, encara és més complicat demostrar que no és solució de cap equació polinòmica amb coeficients enters. Va caldre encara més d'un segle d'esforços per a establir aquesta transcendència.^[37] Aquesta clou una vella qüestió, és a dir, si és possible construir amb el regle i el compàs un quadrat d'igual àrea que una circumferència; aquesta pregunta porta el nom de quadratura del cercle. És impossible, ja que tota construcció d'aquesta naturalesa defineix una superfície d'àrea igual a un nombre algebraic.

Geometria algebraica

Resoldre una equació diofàntica polinòmica no és sempre possible només amb les eines de la teoria algebraica de nombres. Amb aquest tipus de mètode, Ernst Kummer aconsegueix resoldre, a mitjans del segle xix, gairebé tots els casos inferiors a 100 de la cèlebre equació anomenada últim teorema de Fermat,^[38] però el cas general queda pendent.

Per concloure'l cal la geometria, i més precisament la geometria algebraica. L'equació de l'últim teorema de Fermat s'escriu la manera següent: xⁿ + yⁿ = zⁿ. A condició d'estudiar les solucions en els nombres racionals, es pot dividir entre zⁿ i escriure's l'equació qⁿ + rⁿ = 1. Si q i r es trien entre els nombres complexos, notats aquí C, geomètricament, aquesta equació correspon a una figura de C², es tracta d'una superfície real en un espai de dimensió 4. Vista en l'espai projectiu de C², s'obté una superfície real, submergida en un espai compacte la visualització del qual no és intuïtiva. N'hi ha prou amb conèixer els punts racionals d'aquesta superfície per a permetre concloure sobre les solucions del teorema de Fermat.

La topologia ofereix elements de resposta per a aquesta equació. Una superfície d'aquesta naturalesa té un gènere. Topològicament, pot ser equivalent a una esfera (gènere 0), a un tor (gènere 1) o a una figura amb n forats (gènere n). En el cas d'una varietat algebraica, definida per una equació del tipus P(X, Y), en què P és un polinomi amb coeficients racionals, el gènere de la varietat és una indicació sobre el nombre de solucions. Aquest resultat, que porta el nom de teorema de Faltings, és de la mateixa família d'eines de les que es fan servir per a la demostració del teorema de Fermat.^{[Nota 14]}

Zero d'una funció

Algorisme de cerca dicotòmica

Emprant el teorema del punt fix

Mètode de Newton

En anàlisi matemàtica, ben sovint és impossible intentar resoldre una equació amb tècniques elementals de substitució o transformació, esperant aïllar-ne la variable. I fins i tot quan això es demostra possible, com per a certes equacions algebraiques, si l'objectiu és l'obtenció d'un valor numèric, l'enfocament que es descriu en aquest paràgraf sovint és menys costós computacionalment.^{[Nota 15]} Sempre es pot transformar l'equació en una de la forma f(x) = 0. Per exemple l'equació següent, en què la desconeguda és un nombre real estrictament positiu:

${\displaystyle \sin(x)=\ln \left({\frac {1}{\sqrt {x}}}\right)}$

Es transforma en f(x) = 0 si es posa f(x) = sin(x) + 1/2ln(x). En aquest cas particular, un zero és una solució de l'equació. Seria en va intentar expressar un zero per una fórmula composta de funcions elementals (funcions racionals, funcions exponencials, logarítmiques o trigonomètriques…). En aquest cas, tal expressió no existeix. Caldrà conformar-se a buscar el nombre de zeros, dels intervals que els contenen, així com de les aproximacions d'aquests zeros.^[39]

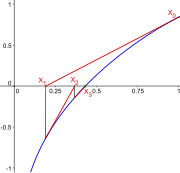
En l'exemple, l'estudi de la funció f mostra fàcilment que hi ha exactament tres zeros, un en l'interval [0, 1], un en [3, 4] i l'últim en [5, 6]. La continuïtat de f permet construir una primera successió (x_n), que convergeix cap al zero de l'interval [0, 1]. Al veïnat de 0, la funció és estrictament negativa, en el punt 1, és estrictament positiva; el teorema del valor intermedi garanteix l'existència d'un zero en aquest interval, ja que f és contínua. Es posa x₀ = 0, en el punt 1/2, la funció f és estrictament positiva; se'n dedueix l'existència d'un zero en l'interval [0, 1/2] i es posa x₁ = 0. En el punt 1/4, és estrictament negativa; se'n dedueix l'existència d'un zero en [1/4, 2/4] i es posa x₂ = 1/4 així successivament. Es construeix així una successió que convergeix cap a la solució, cosa que permet obtenir-ne una aproximació tan precisa com es vulgui. Aquest mètode porta el nom de cerca dicotòmica i és el primer que s'il·lustra a la figura de dalt.^[40]

En l'algoritme precedent, només s'ha fet servir la continuïtat de f, el teorema del punt fix és a la base d'un mètode més eficient. Es construeix una funció g (en vermell a la figura del mig) que té per punt fix (és a dir, un punt x tal com g(x) = x) la solució cercada. S'escull g de tal manera que la derivada en el punt fix sigui la més petita possible. Una solució simple és de definir g(x) = x + λ·f(x). En l'exemple, es pot escollir λ igual a -1/2. Aquesta vegada, és més assenyat escollir x₀ igual a 1. Es defineix x_n = g(x_n-1). Si la derivada de g és propera a 0, la convergència és força millor que la de l'algorisme precedent. En l'exemple escollit, la solució és igual a 0,43247... La quarta iteració del primer mètode dona per valor 0,375 mentre que la quarta del punt fix dona 0,4322...^[41]

La derivabilitat de f arreu del seu domini permet posar a punt un algorisme que té una convergència encara millor. El mètode consisteix en: a partir d'un punt x₀, igual a 1 en l'exemple, trobar la solució x₁ de l'equació lineal tangent a la funció f en el punt x₀. Després, es construeix x₂ com la solució de l'equació lineal tangent de la funció f en el punt x₁. En l'exemple estudiat, això s'il·lustra a la figura de la dreta: el valor de x₄ és igual a 0,43246, o sigui, té quatre decimals exactes. Aquest mètode s'anomena mètode de Newton.^[42]

Equació vectorial

Si l'equació pren la forma f(x) = 0, en què f és una funció d'un espai vectorial E amb valors en un espai vectorial F, el vector nul del qual és notat 0, les idees de l'àlgebra lineal encara s'hi poden aplicar parcialment. És possible escollir una base d'E i una de F i expressar f amb l'ajuda de m funcions f_j reals de n variables x_k, en què m és la dimensió de F i n la de E, s'obté el que s'anomena un sistema d'equacions, de la forma següent:

${\displaystyle \quad \left\{{\begin{matrix}f_{1}(x_{1},\cdots x_{n})=0\\f_{2}(x_{1},\cdots x_{n})=0\\\vdots \\f_{m}(x_{1},\cdots x_{n})=0\end{matrix}}\right.}$

S'apliquen les mateixes limitacions que les descrites en el paràgraf precedent. És possible que la tècnica d'aïllament de les variables, que funciona en el cas de l'equació lineal, no hi sigui possible, per exemple si les f_i contenen expressions massa complexes. Algunes de les idees, expressades en el cas en què f és una funció de variable real amb valors reals, es poden adaptar a la geometria d'un espai vectorial de dimensió finita, d'altres no. No existeix un equivalent del teorema dels valors intermediaris per a la nova configuració. En canvi, el teorema del punt fix es generalitza, així com la definició d'una derivada.

La derivada, o més aviat el diferencial de f, es pot fer servir de diverses maneres. La primera és una simple adaptació del mètode de Newton: a partir d'un punt x₀, es resol l'equació lineal tangent en aquest punt, és a dir, Df_x0·h + f(x₀) = 0. El valor x₁ és igual a x₀ + h i es reitera el procés per obtenir una successió. Si E és igual a F i, per permetre una convergència més ràpida, es resol sovint una equació lineal anàloga, però tal que l'aplicació lineal associada defineix un producte escalar. Aquesta astúcia permet una acceleració del temps de tractament de la resolució de les equacions lineals intermèdies, el mètode associat porta el nom de quasi-Newton.^[43]

Un altre mètode consisteix a transformar el conjunt d'arribada en R₊, per exemple equipant F amb un producte escalar i cercant els zeros de la funció g amb valors reals, que a cada x li associa el quadrat de la norma de f(x), o fins i tot el producte escalar de f(x) per x, si E és igual a F. Les dues equacions f(x) = 0 i f(x)² = 0 tenen les mateixes solucions. El problema es transforma per trobar un extrem de la nova funció g. Es comença en un punt x₀ en la direcció de la línia de major pendent, la direcció del qual ve donada pel gradient, i hom s'atura al punt x₁, el mínim de la funció g en la direcció del gradient. Després, es reitera el càlcul.^{[Nota 16]}

Anàlisi funcional

Si l'espai vectorial E és més vast i ja no és de dimensió finita, s'han de fer servir altres idees per a resoldre l'equació. Aquest cas es dona si la desconeguda x designa una funció. Encara més, és en va cercar mètodes sistemàtics per expressar les solucions sota la forma d'una composició de funcions elementals, els casos en què tals expressions existeixen són més l'excepció que la regla.

Un mètode general^[44] consisteix a associar a un espai de funcions H_p, com el de les funcions contínues definides sobre un interval [a, b], una geometria. Per a fer-ho, es pot definir sobre l'espai una distància euclidiana, és a dir, definida per un producte escalar com el que, en dues funcions f i g de H_p els hi associa:

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(\mu )g(\mu )\mathrm {d} \mu }$

Amb l'ajuda d'aquesta distància, es construeix una successió de funcions (x_n) que verifica la propietat de Cauchy; és a dir, que si els índexs n i m són prou grans, x_n i x_m són arbitràriament propers. Un exemple en ve donat per l'equació integral, anomenada de Fredholm:^[45]

${\displaystyle (1)\quad F(x)=g\quad {\text{amb}}\quad F:x\rightarrow F_{x}(t)=\int _{a}^{b}K(t,\mu )\,x(\mu )\mathrm {d} \mu }$

La successió (x_n) s'ha construït de tal manera que la distància entre les funcions F_xn(t) i g(t) tendeixi cap a zero. La dificultat és que una successió de Cauchy no convergeix necessàriament en H_p, cosa que ve a dir que aquest espai no és complet. Llavors, se submergeix en un espai H que el conté i que és complet.^[46] Un element de H ja no és una funció, pot ser vist com un element del dual de H_p.^[47] En H, la successió (x_n) convergeix cap a un límit s. Es pot interpretar com una solució de l'equació (1), ja que la distància entre F(s) i g és nul·la. Però s no és una funció; és un ens abstracte, element del dual de H_p, se'n parla de solució feble. Finalment, es demostra que aquest ens abstracte s'identifica amb un element de H_p, és a dir, una a funció que verifica l'equació (1), anomenada solució forta.^{[48][Nota 17]}

La física és l'origen d'unes equacions funcionals particulars: els sistemes dinàmics. Un exemple històricament cèlebre, procedeix de la llei de la gravitació universal. Si es negligeix l'atracció deguda als altres planetes, l'acceleració de la Terra es dirigeix cap al Sol i la seva intensitat és inversament proporcional al quadrat de la distància que separa els dos astres. Aquesta llei física es tradueix en una equació que, una vegada conegudes la posició i la velocitat inicials de la Terra, dona la seva trajectòria, és a dir, la seva posició en funció del temps. Històricament, la capacitat per a preveure la posició exacta dels cometes al segle xviii va ser una confirmació de la teoria de Newton.^{[Nota 18]}

Un sistema que evoluciona i del qual una equació permet conèixer exactament el seu estat en el transcurs del temps, a condició de conèixer el seu estat inicial, es qualifica de dinàmic. Els sistemes dinàmics es poden classificar en tres grans categories. La formulació més simple s'anomena discreta,^{[Nota 19]} l'estat del sistema es descriu en diferents etapes, notades pels enters 0, 1, 2..., k... i la solució n'és una successió (u _k). Aquest tipus de sistema es fa servir per a simular un comportament continu, discretitzant el temps amb l'ajuda d'intervals prou petits perquè la imprecisió generada per aquest mètode resti en límits acceptables. Conèixer la trajectòria exacta d'un cometa suposa tenir en compte l'atracció de tots els cossos del sistema solar. Resoldre l'equació en aquest cas es fa difícil; llavors, es pot suposar que, en un segon, la gravetat és gairebé constant, la trajectòria del cometa és gairebé parabòlica i la seva posició al cap d'un segon es calcula fàcilment, una vegada coneguda la posició dels diferents cossos massius com els planetes o el Sol. Llavors, n'hi ha prou amb recalcular, a cada segon, la nova atracció per obtenir una successió que en dona una aproximació de la trajectòria real. Si (p _k, v _k) designa la parella posició i velocitat del cometa en el segon k, existeix en dues funcions f i g:

${\displaystyle p_{n}=f(p_{n-1},v_{n-1})\quad {\text{i}}\quad v_{n}=g(p_{n-1},v_{n-1})}$

S'obtenen successions definides per recurrència, característica d'un sistema dinàmic discret.^[49]

També és possible seguir un altre camí. Una relació que lliga la posició del cometa amb la seva velocitat instantània (que, en matemàtiques, s'anomena derivada) i la seva acceleració (o derivada segona). Resoldre l'equació permet trobar la trajectòria del planeta.^{[Nota 20]} L'equació pren una forma de la naturalesa següent, anomenada equació diferencial:

${\displaystyle f\left(t,p(t),{\frac {\mathrm {d} p}{\mathrm {d} t}}(t),{\frac {\mathrm {d} ^{2}p}{\mathrm {d} t^{2}}}(t)\right)=0}$

Finalment, l'objectiu pot ser determinar l'estat d'un objecte que no es tradueix en un vector d'un espai de dimensió finita, sinó per una funció, com per exemple l'estat d'una corda vibrant. Es parla d'equació en derivades parcials.^[50]

Equació diferencial

La lletra x aquí designa una funció de variable real i f una funció de n + 1 variables reals. Sigui F la funció que a x li associa la funció t ↦ f(t, x(t), x'(t), x⁽²⁾(t),..., x⁽ⁿ⁾(t)), en què x^(k) és la derivada kèsima de la funció x. Es planteja l'equació F(x) = 0. Aquesta equació s'anomena equació diferencial.

Les solucions, en general, s'estudien sota la «forma de Cauchy», és a dir, associades als valors t₀ ,ξ₀ ,ξ₁,... ,ξ_n-1 tals que una solució verifica:

${\displaystyle {\begin{aligned}&f(t,x,x',\cdots ,x^{(n)})=0\\&{\text{amb}}\\&x(t_{0})=\xi _{0},\\&x'(t_{0})=\xi _{1},\ldots ,x^{(n-1)}(t_{0})=\xi _{n-1}\end{aligned}}}$

La situació és una mica anàloga a la de les equacions polinòmiques. Hi ha una teoria d'equacions diferencials.^[51] Un primer resultat global és el teorema de Cauchy-Lipschitz, que garanteix que, si f és una funció de Lipschitz, existeix una única solució al problema de Cauchy. Resoldre el problema de Cauchy consisteix a determinar la solució d'una equació diferencial que verifica una condició inicial donada.^[52] En certs casos particulars, és possible explicitar-ne directament una solució, com per a l'equació diferencial d'ordre 1 amb variables separades o l'equació diferencial lineal, però no sempre.

L'exemple de dreta il·lustra una solució d'una equació de la forma x' = φ(x), en què la solució que s busca és una funció que defineix una corba del pla. La seva variable és real i té valors en R². La funció φ és una funció contínua de R² en R². A cada punt del pla, li associa un vector, s'anomena camp vectorial. Una solució s té la propietat de tenir, per a cada punt p de la seva imatge, una tangent a la corba de direcció φ(p). La velocitat escalar a l'instant t^{[Nota 21]} és igual a la norma de la imatge per φ del punt s(t).

Equació en derivades parcials

La física proposa diversos exemples en què la solució buscada no depèn d'una, sinó de diverses variables. Un cas relativament simple és el d'una ona sobre una corda vibrant. La funció que descriu la seva posició depèn de dos paràmetres, el temps i una coordenada per a descriure un punt de la corda. Per a descriure una ona calen tres variables, dues en descriuen la posició d'un punt de la superfície, i la tercera el temps. En física quàntica, la relació fonamental de la dinàmica es tradueix per una equació d'ona que requereix quatre variables, tres per a l'espai i una pel temps. Aquest principi fonamental s'anomena equació de Schrödinger.

L'equació equivalent a la del paràgraf precedent, per a una funció x de diverses variables, s'anomena equació en derivades parcials. L'equivalent del problema de Cauchy s'expressa de manera més complexa. la condició inicial és reemplaçada per les condicions de contorn. En certs casos, se cerca com a solució una funció definida sobre Ω × [a, b] en què Ω és un obert que se suposa fitat, connex i tal que la seva frontera és regular,^{[Nota 22]} a, b és un interval que representa el temps. Les condicions de contorn s'expressen en forma de dues restriccions. L'una correspon al valor o el límit de la funció sobre ∂Ω × ]a, b[. La funció que modelitza els moviments d'una membrana de tambor és constant al contorn de la membrana; aquesta restricció s'anomena la condició de contorn de Dirichlet. Els valors de la funció sobre Ω × {a} s'anomenen la condició inicial o dada de Cauchy.^[53]

En meteorologia, la previsió numèrica del temps consisteix a modelitzar els moviments de l'atmosfera terrestre per les equacions de Navier-Stokes.^[54] Una dificultat pràctica és la de determinar amb precisió la dada de Cauchy: caldria mesurar la temperatura, la pressió, la humitat, etc., en tot punt de l'atmosfera. Aquesta dificultat, afegida al fet que no se sàpiga resoldre l'equació de Navier-Stokes, fan que els mètodes de resolució emprats siguin numèrics: no se'n poden calcular més que valors aproximats.^[55]

Certes equacions en derivades parcials no són tan complexes. Fourier, un matemàtic de començament del segle xix, havia trobat com es difon la calor en un cos sòlid en el cas de condicions de contorn simples.^[56] L'especificitat d'aquesta equació, com la que descriu les ones que es propaguen sobre una corda vibrant, és de ser lineal, és a dir, que se la pot posar sota la forma a(x) + b = 0, en què a és un operador lineal construït amb l'ajuda de derivades parcials, i b una funció particular. El cas lineal se'n tracta amb una teoria «relativament ben constituïda».^[57] L'eina principal és un espai funcional particular, anomenat de Sobolev.

Altres equacions continuen sent de difícil accés. La superfície d'un oceà també es modelitza per una equació en derivades parcials. Com fa pensar la forma d'una ona, l'expressió d'una solució es pot mostrar difícil.^{[Nota 23]} S'està lluny de disposar-ne d'una teoria general;^[58] els dos apartats que segueixen indiquen el tipus de dificultats a resoldre per comprendre els sistemes dinàmics.

Condició inicial

Una de les qüestions que es formula sobre els sistemes dinàmics és la naturalesa de la solució en funció del seu valor inicial. Si una petita modificació d'aquest valor canvia de manera important el comportament de la solució, fins i tot si el sistema és determinista, la seva evolució semblarà aleatòria. Determinista significa que tota evolució del sistema depèn de manera única del seu valor inicial; el coneixement perfecte d'aquest valor inicial permet preveure perfectament el seu futur, cosa que és sempre el cas d'un sistema dinàmic. En física, és impossible conèixer perfectament l'estat inicial del sistema. Se'l coneix, per exemple amb una precisió de 5 decimals; si el sisè decimal acaba modificant l'evolució del sistema de manera significativa, el futur de l'evolució no és perfectament conegut, sinó que depèn d'una informació inaccessible i el futur apareix com a incert, fins i tot si les lleis que modelitzen l'evolució són deterministes. Aquest fenomen es produeix en meteorologia; aquesta ciència està modelitzada per un sistema dinàmic que, per a permetre una previsió a llarg termini, necessita un coneixement precís de l'estat inicial. Com que aquest coneixement és d'una precisió limitada, existeix un horitzó en la previsió.^[59] Si bé l'equació que modelitza la meteorologia és ben coneguda, no se sap sempre si les solucions depenen contínuament dels valors a les fronteres del domini de la solució (l'equivalent s és la condició inicial per a una equació a les derivades parcials); aquesta qüestió correspon a un dels set premis d'un milió de dòlars oferts per l'Institut de Matemàtiques Clay al primer que n'aporti la resposta.^[60]

Un mètode per apropar-se a la resposta és estudiar-ne els casos més simples possibles. S'intenta comprendre aquest fenomen sobre una successió recurrent definida per l'equació: x_n+1 = f(x_n) en què f és un polinomi de segon grau, real o complex. Un cas molt estudiat és el de f(x) = x² + c. Aquí, la condició inicial és el valor de x₀, un nombre complex. J_c és el conjunt de les condicions inicials tals que la successió és fitada, s'anomena conjunt de Julia, un exemple del qual s'il·lustra a la figura de l'esquerra. Tota condició inicial p fora de la frontera de J_c té un veïnat que no conté més que condicions inicials tals que el comportament de les successions que els hi correspon són qualitativament anàlogues. Els colors indiquen els valors de convergència, la intensitat simbolitza la velocitat de convergència.^[61]

Una primera qüestió que es planteja és el pes de la zona frontera. Sobre aquesta zona, existeix sempre una pertorbació de la condició inicial, per mínima que sigui, que modifica la naturalesa de la solució. En les configuracions clàssiques, una frontera d'una figura geomètrica de dimensió 2 té àrea nul·la, fins i tot si la figura té una àrea estrictament positiva. Així, un cercle de radi estrictament positiu és d'àrea estrictament positiva i la seva frontera, una circumferència d'igual radi, té àrea nul·la. En canvi, la circumferència, considerada com una corba, té una longitud finita. Per la frontera del conjunt de Julia, aquest mètode es mostra de vegades inoperant; es pot trobar una longitud infinita, si la frontera es considera com una corba.^[62] Per a avaluar el pes d'aquesta longitud, es fa servir una observació geomètrica. Sigui S una superfície d'àrea s, l'homotècia de relació 2 aplicada a S defineix una nova superfície d'àrea 2²·s. Si V és una figura geomètrica de dimensió 3 i de volum v, l'homotècia de relació 2 defineix una figura de volum 2³·v. L'exponent que s'aplica a la relació d'homotècia indica la dimensió de la figura, cosa que, en certa manera, permet una avaluació del pes de la figura: es parla de dimensió de Hausdorff o de dimensió fractal.^[63] Aquesta tècnica es pot aplicar a la frontera del conjunt de Julia; la seva dimensió és, en general, diferent d'1:^[64] la frontera s'anomena fractal.^[65]

Caos

La sensibilitat a la condició inicial no és l'única qüestió a resoldre per a elaborar una teoria general dels sistemes dinàmics. També es desitja conèixer el comportament límit del sistema, també anomenat comportament asimptòtic; és a dir, el que es dona una vegada que s'ha esperat que el sistema s'estabilitzi. Si no divergeix, es pot classificar el seu comportament en tres categories, o bé el sistema s'atura en un determinat estat, o bé tendeix cap a una evolució cíclica entre un conjunt d'estats, o bé cap a una altra cosa que, segons certes definicions, s'anomena caos.^[66]

A més, és útil considerar el sistema dinàmic més simple possible, per a comprendre pel cap baix qualitativament els mecanismes que hi entren en joc. Com abans, es fa servir una successió recurrent definida per un polinomi del segon grau P_r, aquesta vegada real amb valors reals. La successió logística es defineix per recurrència: x_r,n+1 = r·x_r,n.(1 - x_r,n). Un dels encants d'aquesta successió és que el seu comportament és relativament independent de la condició inicial si s'escull entre 0 i 1.^{[Nota 24]}

L'objectiu n'és augmentar el valor de r, al començament nul, i estudiar aquest comportament asimptòtic. Si una funció f té un punt fix p_f, amb derivada estrictament compresa entre -1 i 1, en valor absolut, i si la successió definida per x_n+1 = f(x_n) pren un valor proper a aquest punt fix, llavors convergeix cap a p_f. Aquest punt s'anomena atractor i la zona dels valors inicials on les successions convergeixen cap a aquest punt s'anomena conca d'atracció. Per a una successió logística, la conca d'atracció principal conté sempre [0, 1], tret d'un conjunt de mesura nul·la, sigui quin sigui el valor de l'atractor. La successió sembla atreta, com per un imant, cap a aquest atractor. Si r està comprès entre 0 i 3, l'atractor és un punt i la successió convergeix. A partir del valor 3, el polinomi P_r ja no té punt fix, però el polinomi compost amb ell mateix, en té un, si r és prou petit. El comportament asimptòtic de la successió és una oscil·lació entre els dos punts fixos atractius de P_r². El valor 3 de r s'anomena una bifurcació. L'atractor esdevé un conjunt de dos elements, il·lustrat a la figura de la dreta. En el punt 1+√6, es produeix una nova bifurcació; l'atractor té llavors 4 punts. El cardinal de l'atractor augmenta cada vegada més en funció de r duplicant-se, fins a atènyer un valor infinit per a r igual a μ, que se situa entorn de 3,57.^[67]

Es fa necessari precisar el que s'entén per «atractor»: és la intersecció dels conjunts A_n on A_n és la clausura (matemàtiques) dels punts x _k per a k superior a n. En el cas de la successió logística i a excepció d'un conjunt de mesura nul·la, l'atractor és independent de la condició inicial. Es pot veure l'atractor A_r com un conjunt que atreu els elements de la successió, la qual, a partir d'un cert rang, esdevé arbitràriament propera a A. Entre μ i 4, és possible un triple comportament. Per a un conjunt H (d'«hiperbòlic»^[68]) de valors del paràmetre r que és un obert des de [μ, 4], l'atractor és un conjunt finit^[69] (comportament cíclic). Per a un altre conjunt C (de «caòtic»^[70]) de valors del paràmetre, que és tancat, totalment discontinu i de mesura estrictament positiva, per a gairebé tots els valors inicials x₀ (depenent de r), l'atractor és un interval d'interior no buit i el comportament n'és caòtic,^[71] és a dir, que evoluciona sense ordre aparent, a excepció d'un conjunt de mesura nul·la, semblant, que evoluciona a l'atzar, fins i tot si aquesta evolució és, de fet, determinista. L'últim comportament es produeix sobre el conjunt A, complementari de la unió de C i de H en [μ, 4]. El conjunt A no és buit; el comportament és, llavors, més complex i fa intervenir, com a atractor, els conjunts de Cantor.^{[Nota 25]} Des del 2002, se sap que A és de mesura nul·la.^[72]

Aquest comportament s'aplica també a les equacions diferencials o a les equacions en derivades parcials. Edward Lorenz ha trobat una equació diferencial relativament simple, que té un atractor fractal, generalment qualificat d'estrany, i es representa a la segona il·lustració d'aquest article.^[73] Certes equacions diferencials no poden tenir solucions tan complexes; el teorema de Poincaré-Bendixson mostra una família d'equacions que no tenen comportament caòtic.^[74] Solucions caòtiques complexes apareixen també en les equacions de derivades parcials; se les troba en les modelitzacions dels moviments de les masses d'aire, per exemple al voltant de les ales d'un avió, que prenen la forma de turbulències. El 2009, l'estat de les matemàtiques està lluny de ser capaç de presentar una condició necessària i suficient general, que indiqui si hi apareix o no un comportament caòtic, fins i tot en el cas dels sistemes discrets.